File:Ack3a600.jpg
Original file (5,130 × 1,793 pixels, file size: 1.09 MB, MIME type: image/jpeg)
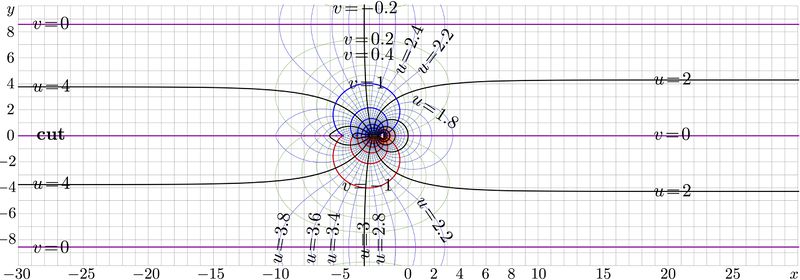
Complex map of tetration to base $b\!=\!\sqrt{2}\!\approx\!1.41$
$u\!+\!\mathrm i v=\mathrm{tet}_b(x\!+\!\mathrm i y)$
C++ Generator of map]
Files ado.cin, conto.cin, sqrt2f21e.cin should be loaded to the working directory in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
#define z_type std::complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "sqrt2f21e.cin"
//#include "tet2f4c.cin"
#include "conto.cin"
int main(){ int j,k,m,m1,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
//z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int M=601,M1=M+1;
int N=461,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
// FILE *o;o=fopen("20.eps","w");ado(o,602,202);
// FILE *o;o=fopen("tet2ma.eps","w");ado(o,602,202);
FILE *o;o=fopen("tetqma.eps","w");ado(o,602,202);
fprintf(o,"301 101 translate\n 10 10 scale\n");
DO(m,M1)X[m]=-30.+.1*(m);
DO(n,200)Y[n]=-10.+.05*n;
Y[200]=-.01;
Y[201]= .01;
for(n=202;n<N1;n++) Y[n]=-10.+.05*(n-1.);
for(m=-30;m<31;m++){if(m==0){M(m,-10.2)L(m,10.2)} else{M(m,-10)L(m,10)}}
for(n=-10;n<11;n++){ M( -30,n)L(30,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(n,N1){y=Y[n];
for(m=295;m<305;m++)
{x=X[m]; //printf("%5.2f\n",x);
z=z_type(x,y);
// c=tetb(z);
// c=F4(z);
c=F21E(z);
p=Re(c);q=Im(c);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
d=c;
for(k=1;k<31;k++)
{ m1=m+k*10; if(m1>M) break;
// d=exp(a*d);
d=exp(d*(.5*log(2.)));
p=Re(d);q=Im(d);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m1*N1+n]=p;f[m1*N1+n]=q;}
}
d=c;
for(k=1;k<31;k++)
{ m1=m-k*10; if(m1<0) break;
// d=log(d)/a;
d=log(d)*(2./log(2.));
p=Re(d);q=Im(d);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m1*N1+n]=p;f[m1*N1+n]=q;}
}
}}
fprintf(o,"1 setlinejoin 2 setlinecap\n"); p=1;q=.5;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".02 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".02 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".02 W 0 0 .9 RGB S\n");
for(m=1;m<10;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".08 W .9 0 0 RGB S\n");
for(m=1;m<10;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".08 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".08 W .6 0 .6 RGB S\n");
for(m=-9;m<10;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".08 W 0 0 0 RGB S\n");
// y= 0; for(m=0;m<260;m+=6) {x=-2.-.1*m; M(x,y) L(x-.1,y)}
// fprintf(o,".07 W 1 .5 0 RGB S\n");
// y= 0; for(m=3;m<260;m+=6) {x=-2-.1*m; M(x,y) L(x-.1,y)}
// fprintf(o,".07 W 0 .5 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//system( "ggv fig3.eps");
system("epstopdf tetqma.eps");
system( "open tetqma.pdf");
getchar(); system("killall Preview");
}
Latex Generator of labels]
\documentclass{amsproc}
\usepackage{graphicx} % Use pdf, png, jpg, or eps§ with pdflatex; use eps in DVI mode\usepackage{amssymb}
\usepackage{rotating}
\usepackage{hyperref}
\newcommand \be {\begin{eqnarray}}
\newcommand \ee {\end{eqnarray} }
\newcommand \sx {\scalebox}
\newcommand \rme {{\rm e}} %%makes the base of natural logarithms Roman font
%\newcommand \rme {{e}} %%makes the base of natural logarithms Italics font; choose one of these
\newcommand \rmi {{\rm i}} %%imaginary unity is always roman font
\newcommand \ds {\displaystyle}
\newcommand \bN {\mathbb{N}}
\newcommand \bC {\mathbb{C}}
\newcommand \bR {\mathbb{R}}
\newcommand \cO {\mathcal{O}}
\newcommand \cF {\mathcal{F}}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \nS {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!}
\newcommand \pS {{~}~{~}}
\newcommand \fac {\mathrm{Factorial}}
\newcommand {\rf}[1] {(\ref{#1})}
\newcommand{\iL}[1] {~\label{#1}\pS \rm[#1]\nS} %make the labels visible
%\newcommand{\iL}[1] {\label{#1}} %make the labels invisible; choose one of these options
\newcommand \eL[1] {\iL{#1}\ee}
\newcommand \ing \includegraphics
\newcommand \tet {\mathrm{tet}}
\usepackage{geometry}
\topmargin -94pt
\oddsidemargin -87pt
\paperwidth 618pt
\paperheight 216pt
\begin{document} %\title{AMS Proceedings Series Sample}
\newcommand \mapax {
\put(2,206){\sx{1.2}{$y$}}
\put(2,188){\sx{1.2}{$8$}}
\put(2,168){\sx{1.2}{$6$}}
\put(2,148){\sx{1.2}{$4$}}
\put(2,128){\sx{1.2}{$2$}}
\put(2,108){\sx{1.2}{$0$}}
\put(-6,88){\sx{1.2}{$-2$}}
\put(-6,68){\sx{1.2}{$-4$}}
\put(-6,48){\sx{1.2}{$-6$}}
\put(-6,28){\sx{1.2}{$-8$}}
\put(-1,1){\sx{1.2}{$-30$}}
\put( 49,1){\sx{1.2}{$-25$}}
\put( 99,1){\sx{1.2}{$-20$}}
\put(149,1){\sx{1.2}{$-15$}}
\put(199,1){\sx{1.2}{$-10$}}
\put(252,1){\sx{1.2}{$-5$}}
\put(309,1){\sx{1.2}{$0$}}
\put(329,1){\sx{1.2}{$2$}}
\put(349,1){\sx{1.2}{$4$}}
\put(369,1){\sx{1.2}{$6$}}
\put(389,1){\sx{1.2}{$8$}}
\put(407,1){\sx{1.2}{$10$}}
\put(457,1){\sx{1.2}{$15$}}
\put(507,1){\sx{1.2}{$20$}}
\put(557,1){\sx{1.2}{$25$}}
\put(607,1){\sx{1.2}{$x$}}
}
%\begin{figure}[t]
%\flushright{$b=\sqrt{2}\approx 1.41$}
%\sx{.586}
{\begin{picture}(620,216) \mapax \put(10,10){\ing{tetqma}} %%%%%%%%
\put(22,194){\sx{1.4}{$v\!=\!0$}}
\put(254,206){\sx{1.4}{$v\!=\!-0.2$}}
\put(262,182){\sx{1.4}{$v\!=\!0.2$}}
\put(262,170){\sx{1.4}{$v\!=\!0.4$}}
\put(266,148){\sx{1.4}{$v\!=\!1$}}
\put(261,69){\sx{1.4}{$v\!=\!-1$}}
%
\put(308,158){\sx{1.4}{\rot{66}$u\!=\!2.4$\ero}}
\put(324,158){\sx{1.4}{\rot{53}$u\!=\!2.2$\ero}}
\put(314,138){\sx{1.4}{\rot{-33}$u\!=\!1.8$\ero}}
%
\put(318,61){\sx{1.4}{\rot{-56}$u\!=\!2.2$\ero}}
%
\put(214,12){\sx{1.4}{\rot{80}$u\!=\!3.8$\ero}}
\put(240,12){\sx{1.4}{\rot{83}$u\!=\!3.6$\ero}}
\put(256,12){\sx{1.4}{\rot{85}$u\!=\!3.4$\ero}}
\put(282,16){\sx{1.4}{\rot{90}$u\!=\!3$\ero}}
\put(294,12){\sx{1.4}{\rot{90}$u\!=\!2.8$\ero}}
%
\put(22, 145.6){\sx{1.4}{$u\!=\!4$}} \put(502, 151){\sx{1.4}{$u\!=\!2$}}
\put(25,108.4){\sx{1.4}{\bf cut}} \put(502,108.4){\sx{1.4}{$v\!=\!0$}}
\put(22, 70.4){\sx{1.4}{$u\!=\!4$}} \put(502, 64.6){\sx{1.4}{$u\!=\!2$}}
\put(22, 21){\sx{1.4}{$v\!=\!0$}}
\end{picture}}
\end{document}
Refrences
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2010q2.pdf
http://mizugadro.mydns.jp/PAPERS/2010q2.pdf
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://mizugadro.mydns.jp/BOOK/202.pdf
Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. (In Russian)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 | 5,130 × 1,793 (1.09 MB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: