File:Amosaplot.jpg
Original file (2,092 × 780 pixels, file size: 147 KB, MIME type: image/jpeg)
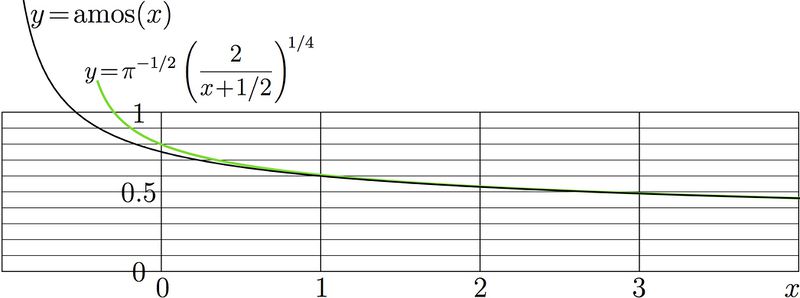
Explicit plot of amplitude of oscillator function, thick black curve, and its asymptotic approximation.
$y=\,$amos$(x)= \displaystyle \frac{e^{-x/2} \,\sqrt{x!}} {\pi^{1/4} (x/2)! }$
C++ generator of cirves
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "fac.cin"
//#include "facp.cin"
//#include "afacc.cin"
//z_type Amp(z_type n){ return sqrt(fac(n)/sqrt(M_PI))/( exp((log(2.)/2.)*n)*fac(.5*n));}
z_type Amp(z_type n){ return exp( -.5*log(2.)*n + (.5*lof(n)-lof(.5*n)) )/sqrt(sqrt(M_PI));}
z_type Ama(z_type n){ DB c[22]= {1, -0.125, 0.0078125 , 0.0205078125 ,
-0.0025939941406250, -0.02483749389648438, 0.003335237503051758,
0.07567062973976135, -0.009997612331062555, -0.4298963562468998,
0.05568409210172831, 3.922531476012864, -0.5014786647962097,
-52.47756609951033, 6.657774463390167, 967.8787886035127,
-122.2445554325703, -23538.53880986894, 2964.833600121925,
729848.1121739772,-91766.94357152004,-2.810206798285763e7};
z_type s; int m,M=21; s=c[M]; for(m=M-1;m>0;m--){s/=n; s+= c[m];} return (1.+s/n)*sqrt((sqrt(2.)/M_PI)/sqrt(n));}
#include "ado.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
for(n=0;n<11;n++) {x=Re(Amp(0.+n));
y=sqrt((sqrt(2.)/M_PI)/sqrt(n+.5));
//t=Re(Ama(0.+n));
printf("%2d %20.14lf %20.14lf %20.14lf\n",n,x,y,x-y);}
#define M(x,y) fprintf(o,"%6.4lf %6.4lf M\n",x+0.,y+0.);
#define L(x,y) fprintf(o,"%6.4lf %6.4lf L\n",x+0.,y+0.);
FILE *o;o=fopen("amosaplo.eps","w");ado(o,504,174);
fprintf(o,"102 2 translate\n 100 100 scale 2 setlinecap 1 setlinejoin\n");
for(m=-1;m<5;m++){ M(m,0)L(m,1) }
for(n=0;n<5;n++){ M( -1,n)L(4,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
for(n=1;n<10;n++){ M( -1,.1*n)L(4,.1*n)}
fprintf(o,".004 W 0 0 0 RGB S\n");
//DO(n,50){ x=-.82+.005*(n*n); y=Re(Amp(x)); if(n==0)M(x,y) else L(x,y);}
DO(n,50){ x=-.86+.002*(n*(n+2)); y=Re(Amp(x)); if(n==0)M(x,y) else L(x,y);}
fprintf(o,".015 W 0 0 0 RGB S\n");
/*
DO(n,59){x=.14+.004*(n*n); y=sqrt((sqrt(2.)/M_PI)/sqrt(x)); if(n==0)M(x,y) else L(x,y); if(x>4) break;}
fprintf(o,".008 W 0 0 1 RGB S\n");
DO(n,59){x=.16+.003*(n*n); y=sqrt((sqrt(2.)/M_PI)/sqrt(x))*(1.-1./8./x); if(n==0)M(x,y) else L(x,y); if(x>4) break;}
fprintf(o,".008 W 1 0 0 RGB S\n");
*/
DO(n,59){x=-.4+.002*(n*n); y=sqrt((sqrt(2.)/M_PI)/sqrt(x+.5)); if(n==0)M(x,y) else L(x,y); if(x>4) break;}
fprintf(o,".008 W 0 .8 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf amosaplo.eps");
system( "open amosaplo.pdf"); //for LINUX
// getchar(); system("killall Preview");//for mac
}
Latex generator of labels
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 504pt
\paperheight 188pt
\topmargin -96pt
\oddsidemargin -73pt
\pagestyle{empty}
\usepackage{graphicx}
\usepackage{rotating}
\parindent 0pt
\textwidth 800px
\textheight 900px
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{document}
\begin{picture}(506,160)
\put(0,0){\includegraphics{amosaplo}}
%\put(20,10){\includegraphics{amosma}}
%\put(20,10){\includegraphics{lofma}}
%\put(20,10){\includegraphics{hermiga6ma}}
%\put(20,10){\includegraphics{hermiten6draft}}
%\put(84,116){\sx{1.5}{$y$}}
\put(84,96){\rot{0}\sx{1.5}{$1$}\ero}
\put(77,46){\rot{0}\sx{1.5}{$0.5$}\ero}
\put(84,-4){\rot{0}\sx{1.5}{$0$}\ero}
\put(99,-14){\rot{0}\sx{1.5}{$0$}\ero}
\put(199,-14){\rot{0}\sx{1.5}{$1$}\ero}
\put(299,-14){\rot{0}\sx{1.5}{$2$}\ero}
\put(399,-14){\rot{0}\sx{1.5}{$3$}\ero}
\put(495,-14){\rot{0}\sx{1.5}{$x$}\ero}
%
\put(20,159){\sx{1.5}{$y\!=\!\mathrm{amos}(x)$}}
%\put(50,122){\sx{1.5}{$y\!=\! (2/(x\!+\!1/2))^{1/4}\pi^{-1/2}$}}
\put(54,124){\sx{1.3}{$\displaystyle y\!=\! \pi^{-1/2} \left( \frac{2}{x\!+\!1/2}\right)^{\!1/4}$}}
%\put(104,21){\sx{1.4}{$y\!=\! (2/x)^{1/4}\pi^{-1/2}(1-\frac{1}{8x})$}}
%\put(104,18.4){\sx{1.5}{$y\!=\! (2/x)^{1/4}\pi^{-1/2}(1-\frac{1}{8x})$}}
\end{picture}
\end{document}
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 | 2,092 × 780 (147 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.