File:E1eiterT.jpg
Original file (2,166 × 2,179 pixels, file size: 1.03 MB, MIME type: image/jpeg)
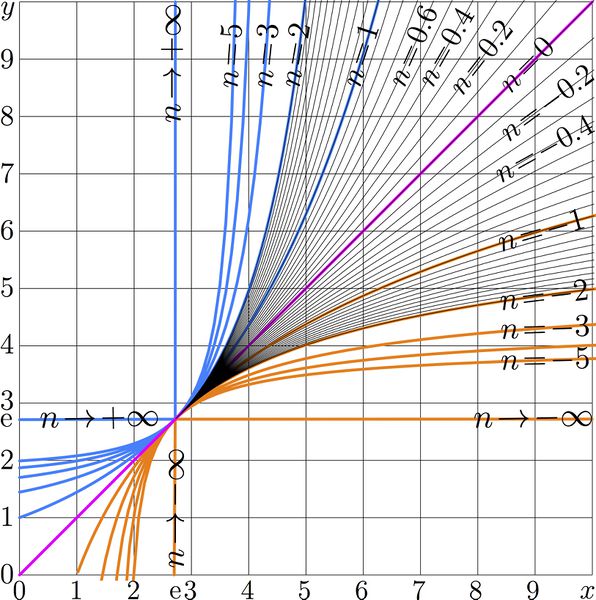
Iterate of exponential to the Henryk base $\eta=\exp(1/\mathrm e)$;
id ess, the iterates of the transfer function $T(z)=\exp(z/\mathrm e)$.
The iterates are expressed through the growing superexponential $F_3$ whih is specific solution of the transfer equation
$F_3(z\!+\!1)=T( F_3(z))$
and the inverse function $G_3=F_3^{-1}$ .
The graphic shows
$y=T^n(x)=F_3(n+G_3(x))$
versus real $x$ for various values $n$. Thick curves correspond to the integer values of $n$
C++ generator of curves
// Files e1etf.cin, e1egf.cin, e1eti.cin, e1egi.cin should be loaded to the working directory in order to compile the code below:
//
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "e1etf.cin"
#include "e1egf.cin"
#include "e1eti.cin"
#include "e1egi.cin"
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//#include "ado.cin"
#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
#define o(x,y) fprintf(o,"%6.3f %6.3f o\n",0.+x,0.+y);
int main(){ int j,k,m,n; DB p,q,t1,t3,u,v,w,x,y; z_type z,c,d;
FILE *o;o=fopen("e1eiter.eps","w");ado(o,1020,1020);
fprintf(o,"10 10 translate\n 100 100 scale\n");
for(m=0;m<11;m++){M(m,0)L(m,10)}
for(n=0;n<11;n++){M(0,n)L(10,n)} fprintf(o,".01 W 0 0 0 RGB S\n");
//M(-3,0)L(20.2,0) M(0, -2)L(0,10.2) fprintf(o,".03 W 0 0 0 RGB S\n");
M(0,M_E)L(M_E,M_E)L(M_E,0) fprintf(o,".006 W 0 0 0 RGB S\n");
fprintf(o,"1 setlinejoin 1 setlinecap\n");
DO(m,101){x=.1*m; y=exp(x/M_E); if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,101){x=.1*m; y=exp(exp(x/M_E)/M_E); if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,101){x=.1*m; y=x; DO(n,3)y=exp(y/M_E); if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,101){x=.1*m; y=x; DO(n,4)y=exp(y/M_E); if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,101){x=.1*m; y=x; DO(n,5)y=exp(y/M_E); if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
M(0,2.71)L(M_E,M_E)L(2.72,10)
fprintf(o,".05 W 0 .5 1 RGB S\n");
DO(m,200){x=1.02+.1*m; y=log(x)*M_E; if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,200){x=1.4+.1*m; y=log(log(x)*M_E)*M_E; if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,200){x=1.6+.1*m; y=x; DO(n,3) y=log(y)*M_E; if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,200){x=1.82+.1*m; y=x; DO(n,4) y=log(y)*M_E; if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
DO(m,200){x=1.98+.1*m; y=x; DO(n,5) y=log(y)*M_E; if(m==0)M(x,y)else L(x,y) if(y>10.) break; }
M(2.7,0)L(M_E,M_E)L(10,2.72)
fprintf(o,".05 W 1 .5 0 RGB S\n");
M(0,0)L(10,10)
fprintf(o,".05 W 1 0 1 RGB S\n");
for(n=-20; n< 21; n++){ DB q=.1*n;
DO(m,200){x=M_E+.01+.1*m; y=Re( E1EGF(q+E1EGI(x)) ); if(m==0)M(x,y)else L(x,y) if(y>10.||x>10.) break; }
}
fprintf(o,".01 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
system("epstopdf e1eiter.eps");
system( "open e1eiter.pdf"); //mac
getchar(); system("killall Preview");// mac
}
//
Latex generator of labels
%
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 1044pt
\paperheight 1050pt
\topmargin -92pt
\oddsidemargin -72pt
\textwidth 1604pt
\textheight 1604pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document}
{\begin{picture}(1042,1024)
\put(1,1016){\sx{4.2}{$y$}}
\put(0,922){\sx{4.2}{$9$}}
\put(0,822){\sx{4.2}{$8$}}
\put(0,722){\sx{4.2}{$7$}}
\put(0,622){\sx{4.2}{$6$}}
\put(0,522){\sx{4.2}{$5$}}
\put(0,422){\sx{4.2}{$4$}}
\put(0,324){\sx{4.2}{$3$}}
\put(0,294){\sx{4.2}{$\mathrm e$}}
\put(0,220){\sx{4.2}{$2$}}
\put(0,120){\sx{4.2}{$1$}}
\put(0,20){\sx{4.2}{$0$}}
\put(22,-8){\sx{4}{$0$}}
\put(122,-8){\sx{4}{$1$}}
\put(222,-8){\sx{4}{$2$}}
\put(297,-7){\sx{4}{$\mathrm e$}}
\put(322,-8){\sx{4}{$3$}}
\put(422,-8){\sx{4}{$4$}}
\put(522,-8){\sx{4}{$5$}}
\put(622,-8){\sx{4}{$6$}}
\put(722,-8){\sx{4}{$7$}}
\put(822,-8){\sx{4}{$8$}}
\put(922,-8){\sx{4}{$9$}}
\put(1016,-7){\sx{4.1}{$x$}}
%\put(0815,520){\sx{5.6}{\rot{78}$y\!=\!\exp(x)$\ero}}
%\put(1118,678){\sx{4.5}{\rot{69}$y\!=\!\eta^x$\ero}}
%\put(1076,606){\sx{4.1}{\rot{67}$y\!=\!\exp_{\eta}(x)$\ero}}
\put(24,24){\ing{e1eiter}}
%\put(10,10){\ing{expe1eplot}}
\put(316,826){\sx{4.9}{\rot{90}$n\!\rightarrow\!+\infty$\ero}}
\put(322, 46){\sx{4.9}{\rot{90}$n\!\rightarrow\!-\infty$\ero}}
\put(416,886){\sx{4.6}{\rot{86}$n\!=\!5$\ero}}
\put(476,886){\sx{4.6}{\rot{84}$n\!=\!3$\ero}}
\put(524,886){\sx{4.6}{\rot{80}$n\!=\!2$\ero}}
\put(630,886){\sx{4.6}{\rot{72}$n\!=\!1$\ero}}
\put(708,886){\sx{4.4}{\rot{66}$n\!=\!0.6$\ero}}
\put(758,886){\sx{4.4}{\rot{60}$n\!=\!0.4$\ero}}
\put(810,872){\sx{4.4}{\rot{52}$n\!=\!0.2$\ero}}
\put(894,876){\sx{4.6}{\rot{45}$n\!=\!0$\ero}}
\put(891,792){\sx{4.4}{\rot{36}$n\!=\!-0.2$\ero}}
\put(878,720){\sx{4.4}{\rot{29}$n\!=\!-0.4$\ero}}
\put(878,600){\sx{4.6}{\rot{16}$n\!=\!-1$\ero}}
\put(878,498){\sx{4.6}{\rot{ 7}$n\!=\!-2$\ero}}
\put(878,448){\sx{4.6}{\rot{ 2}$n\!=\!-3$\ero}}
\put(878,394){\sx{4.6}{\rot{1}$n\!=\!-5$\ero}}
\put(70,292){\sx{4.9}{\rot{1}$n\!\rightarrow\!+\infty$\ero}}
\put(830,292){\sx{4.9}{\rot{1}$n\!\rightarrow\!-\infty$\ero}}
\end{picture}}
\end{document}
References
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf Journal version (the registration may be required)
http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf offprint
http://mizugadro.mydns.jp/PAPERS/2011e1e.pdf (preprint)
https://bitbucket.org/bo198214/e1e/raw/64beab23fa73/main.pdf
H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:11, 1 December 2018 |  | 2,166 × 2,179 (1.03 MB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.