File:LambertWmap150.png

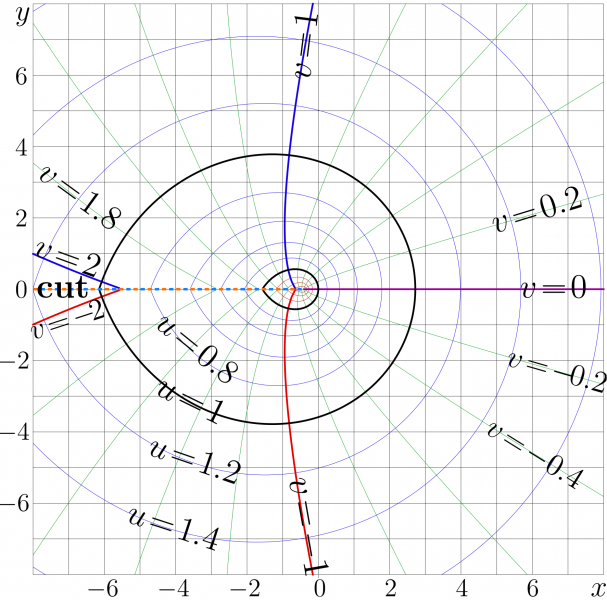
Complex map of the LambertW function.

$f=\mathrm{LambertW}(x\!+\!\mathrm i y)$ is shown with levels

$\Re(f)=u=\mathrm{const~}$ and $\Im(f)=v=\mathrm{const~}$.

The representation through the Tania function is used.

Generators

C++ generator of curves

Files ado.cin and conto.cin should be loaded to the working directory in order to compile the code below:

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"

z_type ArcTania(z_type z) {return z + log(z) - 1. ;}
z_type ArcTaniap(z_type z) {return 1. + 1./z ;}

z_type TaniaTay(z_type z) { int n; z_type s;
s=1.+z*(.5+z*(1./16.+z*(-1./192.+z*(-1./3072.+z*(1.3/6144.+z*(-4.7/147456.
//+z*(7.3/4128768.) //some reserve term
)))))); DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaNega(z_type z){int n;z_type s=exp(z-exp(z)+1.); 
DO(n,4) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaBig(z_type z){int n;z_type s=z; s=z-log(s)+1.; 
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t);
s=-1.+t*(3.+t*(-3.+t*(.75+t*(.3+t*(.9/16.+t*(-.3/7.+t*(-12.51/224. //+t*(-.9/28.)
)))))));
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }

z_type Tania(z_type z){ z_type t;
if( fabs(Im(z))< M_PI && Re(z)<-2.51) return TaniaNega(z);
if( abs(z)>7. || Re(z)>3.8 ) return TaniaBig(z);
if( Im(z) > .7 ) return TaniaS(z);
if( Im(z) < -.7) return conj(TaniaS(conj(z)));
return TaniaTay(z);
}

main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
 int M=160,M1=M+1;
 int N=161,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("productlogmap.eps","w");ado(o,162,162);
fprintf(o,"81 81 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-8.+.1*(m);
DO(n,80)Y[n]=-8.+.1*n;
        Y[80]=-.033;
        Y[81]= .033;
for(n=82;n<N1;n++) Y[n]=-8.+.1*(n-1.);
for(m=-8;m<9;m++){if(m==0){M(m,-8.5)L(m,8.5)} else{M(m,-8)L(m,8)}}
for(n=-8;n<9;n++){     M(  -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);        
 c=Tania(log(z)-1.); p=Re(c);q=Im(c);  
 if(p>-99. && p<99. &&  q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
        }}
fprintf(o,"1 setlinejoin 2 setlinecap\n");  p=.6;q=.5;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".01 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".01 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".01 W 0 0 .9 RGB S\n");
for(m=1;m<10;m++)  conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".05 W .9 0 0 RGB S\n");
for(m=1;m<10;m++)  conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 .9 RGB S\n");
                   conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p); fprintf(o,".05 W .6 0 .6 RGB S\n");
for(m=-9;m<10;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 0 RGB S\n");
y=0.; for(m=0;m<75;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 1 .5 0 RGB S\n");
y=0.; for(m=2;m<75;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 0 .5 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
       system("epstopdf productlogmap.eps");   
       system(    "open productlogmap.pdf");
       getchar(); system("killall Preview");
}

Latex generator of lables

References

http://mathworld.wolfram.com/LambertW-Function.html