File:Nem1it.jpg
Original file (1,519 × 2,349 pixels, file size: 1.14 MB, MIME type: image/jpeg)
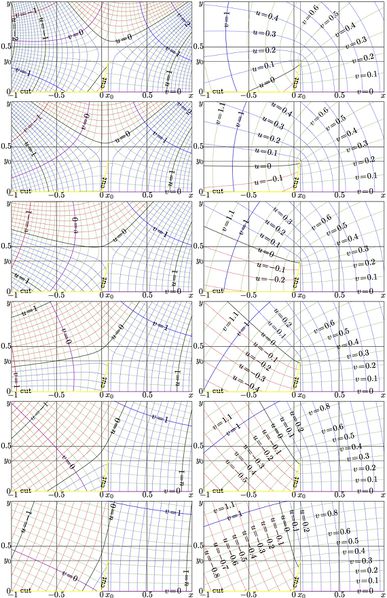
Complex maps of iterates of the Nemtsov function with parameter $q=1$
$u\!+\!\mathrm i v=\mathrm{Nem}_1^{\,n}(x\!+\!\mathrm i y)$
for $n=0.6$, $n=0.5$, $n=0.4$, $n=0.3$, $n=0.2$, $n=0.1$, left column, and for
$n=-0.6$, $n=-0.5$, $n=-0.4$, $n=-0.3$, $n=-0.2$, $n=-0.1$,
right column
C++ generator of the first map
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
DB Q=1.;
z_type nem(z_type z){ return z*(1.+z*z*(1.+z*Q)); }
z_type nem1(z_type z){ return 1.+z*z*(3.+z*(4.*Q)); } // WARNING: Q is global!
#include "sune.cin"
DB SUNo=0.;
z_type sunem(z_type z){ return sune(z + SUNo);}
#include"nembran.cin"
z_type NemZo=nembra(Q);
z_type ANemZo=nem(NemZo);
DB tr=Re(ANemZo);
DB ti=Im(ANemZo);
#include "arqnem.cin"
DB C[41];
//DB K=Q*Q;
int coa(){ //C[1]=(0.5 - K)*Q; C[2]=-0.625 + (-0.25 + K/2.)*K; ..
#include "aunemco.txt"
return 40;
}
z_type aune0(z_type z){ z_type s; int n;
s=C[40]*z; for(n=39;n>0;n--){s+=C[n];s*=z;}
return (-.5/z+Q)/z + (1.5+K)*log(z) + (.5*K + (.75+.5*K)*log(2.)) + s ;
}
DB AUNE1=0;
z_type aune1(z_type z){ int n, N=20; DO(n,N) z=arqnem(z);
return aune0(z)+(0.+n);}
z_type aunem(z_type z){ int n, N=20; DO(n,N) z=arqnem(z);
return aune0(z)+(n-AUNE1);}
z_type aune02(z_type z){ z_type s; int n; s=(C[2]*z+C[1])*z;
return (-.5/z+Q)/z + (1.5+K)*log(z) + (.5*K + (.75+.5*K)*log(2.)) + s ; }
z_type aune01(z_type z){ z_type s; int n; s=C[1]*z;
return (-.5/z+Q)/z + (1.5+K)*log(z) + (.5*K + (.75+.5*K)*log(2.)) +s ; }
int main(){ int Max; int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
// DB rr,ti;
K=Q*Q; x=0; co(); printf("Q=%9.4lf\n",Q);
DO(n,300) { y=Re(sunem(0)); SUNo-= y-1.; printf("%19.16lf %19.16lf\n", SUNo,y);} // getchar();
co();
coa();
AUNE1=Re(aune1(1.));
//printf("A[2][1]= %9.5f\n",A[2][1]);
printf("A[2][0]= %9.5lf , A[2][1]=%9.5lf\n",A[2][0],A[2][1]);
printf("A[3][0]= %9.5lf , A[3][1]=%9.5lf\n",A[3][0],A[3][1]);
printf("K= %9.5lf , C[1]=%9.5lf\n",K,C[1]);
int M=1001,M1=M+1;
int N=201,N1=N+1;
DB X[M1],Y[N1]; DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
//DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
FILE *o;o=fopen("nem1n6.eps","w");ado(o,2008,1008);
fprintf(o,"1004 4 translate\n 1000 1000 scale 2 setlinecap\n");
DO(m,M1) X[m]=-1.+.002*(m-.5);
DO(n,N1) Y[n]= .005*(n-.5);
for(m=-10;m<11;m+=5){ M(.1*m,0)L(.1*m,1)}
for(n=0;n<11;n+=5){ M(-1,.1*n)L(1,.1*n)}
fprintf(o,".004 W 0 0 0 RGB 2 setlinecap S\n");
M(-1,ti)L(1,ti) M(tr,0)L(tr,1) fprintf(o,".003 W 0 0 0 RGB 2 setlinecap S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999999; f[m*N1+n]=9999999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=aunem(z); c=sunem(.6+c);
//p=abs(c-z)/(abs(c)+abs(z)); p=-log(p)/log(10.);
p=Re(c); q=Im(c);
if(p>-85 && p<85) g[m*N1+n]=p;
if(p>-1001 && p<1001 &&
q >-1001 && q<1001 ) { g[m*N1+n]=p; f[m*N1+n]=q; }
}}
//M(-2,0) L(0,0) M(tr,ti)L(0,0)L(tr,-ti)
//fprintf(o,".002 W 1 1 0 RGB 0 setlinecap S\n");
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=200.;q=2.;
//#include"plofu.cin"
for(m=-5;m<5;m++)for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".001 W 0 .6 0 RGB S\n");
for(m=0;m<5;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);
fprintf(o,".001 W .9 0 0 RGB S\n");
for(m=0;m<5;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".001 W 0 0 .9 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N,(0.-m),-p,p);fprintf(o,".004 W .8 0 0 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".004 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N,(0. ),-p,p);fprintf(o,".004 W .5 0 .5 RGB S\n");
for(m=-10;m<11;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".004 W 0 0 0 RGB S\n");
/*
//conto(o,g,w,v,X,Y,M,N,15.5,-1,1);fprintf(o,".02 W 1 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N,15.,-p,p);fprintf(o,".004 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N,14.,-p,p);fprintf(o,".002 W 0 1 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,13.,-p,p);fprintf(o,".002 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,12.,-p,p);fprintf(o,".004 W 0 0 .7 RGB S\n");
conto(o,g,w,v,X,Y,M,N,11.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,10.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 9.,-p,p);fprintf(o,".004 W 0 .6 .8 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 8.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 7.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 6.,-p,p);fprintf(o,".004 W 0 .6 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 5.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 4.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 3.,-p,p);fprintf(o,".004 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 2.,-p,p);fprintf(o,".002 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, 1.,-p,p);fprintf(o,".005 W .5 0 0 RGB S\n");
*/
M(-1,0) L(0,0) M(tr,ti)L(0,0) L(tr,-ti)
fprintf(o,".008 W 1 1 0 RGB 0 setlinecap S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
system("epstopdf nem1n6.eps");
system( "open nem1n6.pdf"); //mac
return 0;}
Latex combined of the maps and labels
\documentclass{mcom-l}
% \documentclass[12pt]{article}
\usepackage{graphics}
\paperwidth 366pt
\paperheight 566pt
\usepackage{geometry}
\usepackage{rotating}
\textwidth 660pt
\textheight 660pt
\topmargin -96pt
\oddsidemargin -220pt
\pagestyle{empty}
%\parindent 0pt
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{document}
%\pagestyle{empty}
\newcommand \scalite {\put(200,040){\sx{8}{\rot{0.} \bf cut \ero}}
\put(1130,090){\sx{8}{\rot{73} \bf cut \ero}}
\put(50,1022){\sx{9}{$y$}}
\put(-12,536){\sx{9}{$0.5$}}
\put(20,380){\sx{9}{$y_0$}}
\put(50,030){\sx{9}{$0$}}
\put(60, -9){\sx{9}{$-1$}}
\put(510,-9){\sx{9}{$-0.5$}}
\put(1084,-9){\sx{9}{$0$}}
\put(1150,-7){\sx{9}{$x_0$}}
\put(1560, -9){\sx{9}{$0.5$}}
\put(2076, -9){\sx{9}{$x$}}
}
%\url{http://mizugadro.mydns.jp/t/index.php/File:Aunem2ht.jpg}\\
\begin{figure}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n6}}
%\put(770,980){\sx{9}{\rot{-52} $u\!=\!0$\ero}}
\put(110,880){\sx{9}{\rot{-88} $u\!=\!-2$\ero}}
\put(412,880){\sx{9}{\rot{-80} $u\!=\!-1$\ero}}
\put(1270,594){\sx{9}{\rot{17} $u\!=\!0$\ero}}
\put(1850,110){\sx{9}{\rot{77} $u\!=\!1$\ero}}
%
\put(150,880){\sx{9}{\rot{14} $v\!=\!-1$\ero}}
\put(740,640){\sx{9}{\rot{20} $v\!=\!0$\ero}}
\put(140,290){\sx{9}{\rot{-20} $v\!=\!1$\ero}}
%
\put(1940,914){\sx{9}{\rot{-49} $v\!=\!2$\ero}}
\put(1810,534){\sx{9}{\rot{-31} $v\!=\!1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m6}}
\put(680,920){\sx{9}{\rot{-17} $u\!=\!0.4$\ero}}
\put(650,700){\sx{9}{\rot{-7} $u\!=\!0.3$\ero}}
\put(650,486){\sx{9}{\rot{2} $u\!=\!0.2$\ero}}
\put(650,280){\sx{9}{\rot{14} $u\!=\!0.1$\ero}}
\put(730,100){\sx{9}{\rot{23} $u\!=\!0$\ero}}
%
\put(374,770){\sx{9}{\rot{85} $v\!=\!1$\ero}}
\put(1226,800){\sx{9}{\rot{50} $v\!=\!0.6$\ero}}
\put(1420,756){\sx{9}{\rot{40} $v\!=\!0.5$\ero}}
\put(1580,660){\sx{9}{\rot{30} $v\!=\!0.4$\ero}}
\put(1690,530){\sx{9}{\rot{22} $v\!=\!0.3$\ero}}
\put(1760,370){\sx{9}{\rot{14} $v\!=\!0.2$\ero}}
\put(1790,204){\sx{9}{\rot{6} $v\!=\!0.1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n5}}
%\put(640,814){\sx{9}{\rot{-33} $u\!=\!0$\ero}}
\put(1270,596){\sx{9}{\rot{30} $u\!=\!0$\ero}}
\put(244,600){\sx{9}{\rot{-59} $u\!=\!1$\ero}}
\put(1886,110){\sx{9}{\rot{79} $u\!=\!1$\ero}}
%
\put(260,710){\sx{9}{\rot{43} $v\!=\!-1$\ero}}
\put(918,740){\sx{9}{\rot{72} $v\!=\!0$\ero}}
%
\put(1940,1030){\sx{9}{\rot{-41} $v\!=\!2$\ero}}
\put(1670,700){\sx{9}{\rot{-36} $v\!=\!1$\ero}}
%
\put(1810,32){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m5}}
\put(850,1024){\sx{9}{\rot{-32} $u\!=\!0.4$\ero}}
\put(750,860){\sx{9}{\rot{-26} $u\!=\!0.3$\ero}}
\put(700,674){\sx{9}{\rot{-18} $u\!=\!0.2$\ero}}
\put(670,500){\sx{9}{\rot{-10} $u\!=\!0.1$\ero}}
\put(670,314){\sx{9}{\rot{1} $u\!=\!0$\ero}}
\put(670,130){\sx{9}{\rot{10} $u\!=\!-0.1$\ero}}
%
\put(280,800){\sx{9}{\rot{75} $v\!=\!1.1$\ero}}
\put(500,770){\sx{9}{\rot{73} $v\!=\!1$\ero}}
\put(1310,790){\sx{9}{\rot{42} $v\!=\!0.6$\ero}}
\put(1480,730){\sx{9}{\rot{33} $v\!=\!0.5$\ero}}
\put(1590,610){\sx{9}{\rot{26} $v\!=\!0.4$\ero}}
\put(1700,490){\sx{9}{\rot{20} $v\!=\!0.3$\ero}}
\put(1770,340){\sx{9}{\rot{13} $v\!=\!0.2$\ero}}
\put(1790,190){\sx{9}{\rot{5} $v\!=\!0.1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n4}}
\put(1250,600){\sx{9}{\rot{40} $u\!=\!0$\ero}}
\put(1926,110){\sx{9}{\rot{82} $u\!=\!1$\ero}}
\put(126,230){\sx{9}{\rot{-30} $u\!=\!1$\ero}}
\put(284,710){\sx{9}{\rot{80} $v\!=\!-1$\ero}}
\put(840,700){\sx{9}{\rot{90} $v\!=\!0$\ero}}
%
%\put(1940,1030){\sx{9}{\rot{-41} $v\!=\!2$\ero}}
\put(1670,748){\sx{9}{\rot{-30} $v\!=\!1$\ero}}
%
\put(1810,32){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m4}}
\put(870,970){\sx{9}{\rot{-42} $u\!=\!0.3$\ero}}
\put(780,830){\sx{9}{\rot{-36} $u\!=\!0.2$\ero}}
\put(720,676){\sx{9}{\rot{-32} $u\!=\!0.1$\ero}}
\put(700,510){\sx{9}{\rot{-23} $u\!=\!0$\ero}}
\put(690,340){\sx{9}{\rot{-13} $u\!=\!-0.1$\ero}}
\put(680,180){\sx{9}{\rot{-4} $u\!=\!-0.2$\ero}}
%
\put(344,720){\sx{9}{\rot{65} $v\!=\!1.1$\ero}}
\put(530,680){\sx{9}{\rot{64} $v\!=\!1$\ero}}
\put(1320,734){\sx{9}{\rot{33} $v\!=\!0.6$\ero}}
\put(1480,672){\sx{9}{\rot{25} $v\!=\!0.5$\ero}}
\put(1590,566){\sx{9}{\rot{19} $v\!=\!0.4$\ero}}
\put(1700,452){\sx{9}{\rot{14} $v\!=\!0.3$\ero}}
\put(1770,320){\sx{9}{\rot{10} $v\!=\!0.2$\ero}}
\put(1790,174){\sx{9}{\rot{5} $v\!=\!0.1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n3}}
\put(1240,630){\sx{9}{\rot{50} $u\!=\!0$\ero}}
\put(1970,110){\sx{9}{\rot{86} $u\!=\!1$\ero}}
%
\put(1670,800){\sx{9}{\rot{-22} $v\!=\!1$\ero}}
\put(660,750){\sx{9}{\rot{-70} $v\!=\!0$\ero}}
\put(226,894){\sx{9}{\rot{22} $u\!=\!1$\ero}}
%
%
\put(130,270){\sx{9}{\rot{-88} $v\!=\!1$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m3}}
\put(880,960){\sx{9}{\rot{-50} $u\!=\!0.2$\ero}}
\put(810,820){\sx{9}{\rot{-46} $u\!=\!0.1$\ero}}
\put(734,690){\sx{9}{\rot{-42} $u\!=\!0$\ero}}
\put(650,580){\sx{9}{\rot{-39} $u\!=\!-0.1$\ero}}
\put(560,470){\sx{9}{\rot{-35} $u\!=\!-0.2$\ero}}
\put(490,330){\sx{9}{\rot{-31} $u\!=\!-0.3$\ero}}
\put(420,200){\sx{9}{\rot{-28} $u\!=\!-0.4$\ero}}
%
\put(342,720){\sx{9}{\rot{52} $v\!=\!1.1$\ero}}
\put(500,666){\sx{9}{\rot{50} $v\!=\!1$\ero}}
\put(1340,696){\sx{9}{\rot{25} $v\!=\!0.6$\ero}}
\put(1490,630){\sx{9}{\rot{18} $v\!=\!0.5$\ero}}
\put(1590,524){\sx{9}{\rot{15} $v\!=\!0.4$\ero}}
\put(1700,420){\sx{9}{\rot{10} $v\!=\!0.3$\ero}}
\put(1770,300){\sx{9}{\rot{5} $v\!=\!0.2$\ero}}
\put(1790,166){\sx{9}{\rot{2} $v\!=\!0.1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n2}}
\put(338,840){\sx{9}{\rot{45} $u\!=\!-1$\ero}}
\put(1240,686){\sx{9}{\rot{65} $u\!=\!0$\ero}}
\put(2018,110){\sx{9}{\rot{87} $u\!=\!1$\ero}}
%
\put(1660,870){\sx{9.4}{\rot{-16} $v\!=\!1$\ero}}
\put(660,440){\sx{9}{\rot{-52} $v\!=\!0$\ero}}
\put(1800,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m2}}
\put(1060,940){\sx{9}{\rot{-65} $u\!=\!0.2$\ero}}
\put(950,870){\sx{9}{\rot{-62} $u\!=\!0.1$\ero}}
\put(850,800){\sx{9}{\rot{-60} $u\!=\!0$\ero}}
\put(750,730){\sx{9}{\rot{-57} $u\!=\!-0.1$\ero}}
\put(650,660){\sx{9}{\rot{-55} $u\!=\!-0.2$\ero}}
\put(540,560){\sx{9}{\rot{-52} $u\!=\!-0.3$\ero}}
\put(440,480){\sx{9}{\rot{-49} $u\!=\!-0.4$\ero}}
\put(340,390){\sx{9}{\rot{-48} $u\!=\!-0.5$\ero}}
%
\put(220,736){\sx{9}{\rot{34} $v\!=\!1.1$\ero}}
\put(370,670){\sx{9}{\rot{34} $v\!=\!1$\ero}}
\put(1280,900){\sx{9}{\rot{20} $v\!=\!0.8$\ero}}
\put(1420,694){\sx{9}{\rot{14} $v\!=\!0.6$\ero}}
\put(1540,602){\sx{9}{\rot{12} $v\!=\!0.5$\ero}}
\put(1620,500){\sx{9}{\rot{8} $v\!=\!0.4$\ero}}
\put(1700,390){\sx{9}{\rot{8} $v\!=\!0.3$\ero}}
\put(1770,276){\sx{9}{\rot{4} $v\!=\!0.2$\ero}}
\put(1790,154){\sx{9}{\rot{2} $v\!=\!0.1$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1n1}}
\put(244,700){\sx{9}{\rot{70} $u\!=\!-1$\ero}}
\put(1225,840){\sx{9}{\rot{76} $u\!=\!0$\ero}}
\put(2070,110){\sx{9}{\rot{88} $u\!=\!1$\ero}}
%
\put(1810,924){\sx{9}{\rot{-9} $v\!=\!1$\ero}}
\put(660,244){\sx{9}{\rot{-26} $v\!=\!0$\ero}}
\put(1810,34){\sx{9}{\rot{0} $v\!=\!0$\ero}}
%
\end{picture}}
\sx{.085}{\begin{picture}(2100,1100)\scalite \put(100,50){\ing{nem1m1}}
%
\put(1178,960){\sx{9}{\rot{-79} $u\!=\!0.2$\ero}}
\put(1060,960){\sx{9}{\rot{-79} $u\!=\!0.1$\ero}}
\put(964,896){\sx{9}{\rot{-76} $u\!=\!0$\ero}}
\put(850,870){\sx{9}{\rot{-73} $u\!=\!-0.1$\ero}}
\put(740,830){\sx{9}{\rot{-72} $u\!=\!-0.2$\ero}}
\put(630,780){\sx{9}{\rot{-71} $u\!=\!-0.3$\ero}}
\put(530,720){\sx{9}{\rot{-70} $u\!=\!-0.4$\ero}}
\put(420,680){\sx{9}{\rot{-69} $u\!=\!-0.5$\ero}}
\put(320,640){\sx{9}{\rot{-69} $u\!=\!-0.6$\ero}}
\put(210,590){\sx{9}{\rot{-69} $u\!=\!-0.7$\ero}}
\put(110,500){\sx{9}{\rot{-68} $u\!=\!-0.8$\ero}}
%
\put(220,920){\sx{9}{\rot{19} $v\!=\!1.1$\ero}}
\put(370,840){\sx{9}{\rot{19} $v\!=\!1$\ero}}
%\put(1200,956){\sx{9}{\rot{10} $v\!=\!0.9$\ero}}
\put(1350,870){\sx{9}{\rot{8} $v\!=\!0.8$\ero}}
\put(1490,670){\sx{9}{\rot{7} $v\!=\!0.6$\ero}}
\put(1580,570){\sx{9}{\rot{5} $v\!=\!0.5$\ero}}
\put(1650,466){\sx{9}{\rot{3} $v\!=\!0.4$\ero}}
\put(1730,358){\sx{9}{\rot{3} $v\!=\!0.3$\ero}}
\put(1790,254){\sx{9}{\rot{2} $v\!=\!0.2$\ero}}
\put(1800,144){\sx{9}{\rot{1} $v\!=\!0.1$\ero}}
\put(1810,33){\sx{9}{\rot{0} $v\!=\!0$\ero}}
%
\end{picture}}
\vskip -6pt
\caption{ $u\!+\!\mathrm i v=\mathrm{Nem}_1^{\,n}(x\!+\!\mathrm i y)$ for $n=-0.6$ .. $0.6$}
\end{figure}
\end{document}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:13, 1 December 2018 |  | 1,519 × 2,349 (1.14 MB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.