File:Sqrt2srav.png

From TORI
Jump to navigation Jump to search

Original file ‎(2,532 × 1,639 pixels, file size: 263 KB, MIME type: image/png)

Comparison or two half iterate of exponent to base \( \sqrt{2} \) constructed at fixed point 2 and at fixed point 4.

\( y=\exp_{\sqrt{2},\mathrm u}^{~1/2}(x) \) , solid line

\( y=\exp_{\sqrt{2},\mathrm d}^{~1/2}(x) \) , dashed line

The thin curve represents the difference, \(y=D(x)= \exp_{\sqrt{2},\mathrm u}^{~1/2}(x) -\exp_{\sqrt{2},\mathrm d}^{~1/2}(x)\) , scaled with factor \(10^{24} \).

Usage: this is figure 16.9 of the book Суперфункции (2014, In Russian) [1]; the English version is in preparation in 2015.

This image is used also in article [2].


Refereces

  1. ↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
    http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
    http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.
  2. ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
    http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.


C++ generator of the curves

Files ado.cin, conto.cin, sqrt2f23e.cin, sqrt2f23l.cin, sqrt2f43e.cin, sqrt2f43l.cin should be loaded in order to compile the code below.



 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
// #include "conto.cin"
#include "ado.cin"
 #include "sqrt2f23E.cin"
 #include "sqrt2f23L.cin"
 #include "sqrt2f43E.cin"
 #include "sqrt2f43L.cin"
// #include "superex.cin"
// #include "slog14128.cin"

// #include "exq.cin"
z_type exq(z_type z){ DB T4= 19.236149042042854712;
                        DB T2=-17.143148179354847104; z_type z3=z-3.;
// return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.009))*sin(0.75+z3*(-.0767+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.009))*sin(0.75+z3*(-.075+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.47e-25*(z-2.)*(4.-z)*(1.+z3*(.122+z3*.006))*sin(0.74+z3*(-.07+z3*(+.01) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.747+z3*(-.069+z3*(+.007) )+ T4*log(4.-z) + T2*log(z-2.) );

// return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.747+z3*(-.068+z3*(+.007) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.067+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.067+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
// return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.07+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
        return 2.48e-25*(z-2.)*(4.-z)*(1.+z3*(.120+z3*.006))*sin(0.4+z3*(-.08+z3*(-.8) )+ T4*log(4.-z) + T2*log(z-2.) );
                }


DB XI[200]={
2.00, 2.01, 2.02, 2.03, 2.04, 2.05, 2.06, 2.07, 2.08, 2.09, 2.10, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19,
2.20, 2.21, 2.22, 2.23, 2.24, 2.25, 2.26, 2.27, 2.28, 2.29, 2.30, 2.31, 2.32, 2.33, 2.34, 2.35, 2.36, 2.37, 2.38, 2.39,
2.40, 2.41, 2.42, 2.43, 2.44, 2.45, 2.46, 2.47, 2.48, 2.49, 2.50, 2.51, 2.52, 2.53, 2.54, 2.55, 2.56, 2.57, 2.58, 2.59,
2.60, 2.61, 2.62, 2.63, 2.64, 2.65, 2.66, 2.67, 2.68, 2.69, 2.70, 2.71, 2.72, 2.73, 2.74, 2.75, 2.76, 2.77, 2.78, 2.79,
2.80, 2.81, 2.82, 2.83, 2.84, 2.85, 2.86, 2.87, 2.88, 2.89, 2.90, 2.91, 2.92, 2.93, 2.94, 2.95, 2.96, 2.97, 2.98, 2.99,
3.00, 3.01, 3.02, 3.03, 3.04, 3.05, 3.06, 3.07, 3.08, 3.09, 3.10, 3.11, 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, 3.18, 3.19,
3.20, 3.21, 3.22, 3.23, 3.24, 3.25, 3.26, 3.27, 3.28, 3.29, 3.30, 3.31, 3.32, 3.33, 3.34, 3.35, 3.36, 3.37, 3.38, 3.39,
3.40, 3.41, 3.42, 3.43, 3.44, 3.45, 3.46, 3.47, 3.48, 3.49, 3.50, 3.51, 3.52, 3.53, 3.54, 3.55, 3.56, 3.57, 3.58, 3.59,
3.60, 3.61, 3.62, 3.63, 3.64, 3.65, 3.66, 3.67, 3.68, 3.69, 3.70, 3.71, 3.72, 3.73, 3.74, 3.75, 3.76, 3.77, 3.78, 3.79,
3.80, 3.81, 3.82, 3.83, 3.84, 3.85, 3.86, 3.87, 3.88, 3.89, 3.90, 3.91, 3.92, 3.93, 3.94, 3.95, 3.96, 3.97, 3.98, 3.99};

//seq(10000000000000000000000000 eq42i[i], i = 1 .. 199) // multiply the table below with 10^25
DB DI[200]={0.,
 0.4784698105 -0.05393190341, -0.1300677822, -0.03171912709, 0.1785649091,
-0.2250109272, 0.1825902914, 0.03480286362, -0.3467282069, 0.3008735706,
 0.2712188539, -0.4190409114, -0.3490350151, 0.3694646591, 0.5766896417,
-0.02558065033, -0.6509275876, -0.5677290067, 0.1249427107, 0.7445345668,
 0.7404203400, 0.1276956912, -0.6160794452, -0.9628063538, -0.6916022303,
 0.01864447876, 0.7488833086, 1.101226313, 0.9014321358, 0.2561118946,
-0.5300917829, -1.110965026, -1.247875232, -0.8932436694, -0.1889188837,
 0.6042806729, 1.208925529, 1.425359378, 1.188972596, 0.5785454907,
-0.2192350209, -0.9722698076, -1.471223669, -1.584225579, -1.285665934,
-0.6552228513, 0.1488558485, 0.9326874399, 1.514042501, 1.762841619,
 1.626741407, 1.137951659, 0.4018211902, -0.4286446672, -1.185893868,
-1.721405217, -1.933299208, -1.783360064, -1.301259878, -0.5762799943,
 0.2610215297, 1.063258680, 1.692178857, 2.041693575, 2.054394851,
 1.729315148, 1.120250436, 0.3254866584, -0.5289731871, -1.309749251,
-1.896727084, -2.200905751, -2.176957263, -1.828915204, -1.208481545,
-0.4065111531, 0.4608414413, 1.269162309, 1.903518088, 2.274423794,
 2.329910221, 2.062170481, 1.508044374, 0.7434411090, -0.1274043434,
-0.9862966412, -1.717093805, -2.221232577, -2.430741451, -2.317083136,
-1.894734068, -1.219099562, -0.3790914522, 0.5146293821, 1.344202005,
 2.000019677, 2.395098433, 2.476513136, 2.232427985, 1.693805806,
 0.9305534145, 0.04256669434, -0.8532073059, -1.638054138, -2.207164096,
-2.483657197, -2.429103975, -2.049103493, -1.393092023, -0.5482898657,
 0.3715392444, 1.241138307, 1.940691601, 2.372404168, 2.474456697,
 2.230337845, 1.672108541, 0.8769280448, -0.04292211556, -0.9553576726,
-1.727182735, -2.243596738, -2.425705096, -2.243353388, -1.721136622,
-0.9363222889, -.008568273516, 0.9174331778, 1.694075610, 2.194493483,
 2.334032812, 2.085879418, 1.487850807, 0.6385838664, -0.3169989468,
-1.211215472, -1.882663464, -2.205965842, -2.116798723, -1.627093624,
-0.8266252487, 0.1305785338, 1.053731641, 1.752439170, 2.076719446,
 1.951641871, 1.398412552, 0.5356620174, -0.4416412943, -1.303325066,
-1.837659684, -1.905696400, -1.482410042, -0.6719601817, 0.3107105811,
 1.191600113, 1.712573743, 1.710469692, 1.176345414, 0.2724209897,
-0.7061642661, -1.421131980, -1.609137760, -1.188763710, -0.3119998189,
 0.6722631328, 1.345399787, 1.398988810, 0.7938478007, -0.1863084618,
-1.040543314, -1.297193305, -0.7929908943, 0.1807419873, 1.000006240,
 1.091699572, 0.3698400463, -0.6124347228, -1.024247436, -0.4742694444,
 0.5137381025, 0.8869221813, 0.1975127230, -0.6902438791, -0.5357760631,
 0.4270413342, 0.5566459653, -0.3748406966, -0.3814257507, 0.4878409640,
-0.08114350401, -0.2447048034, 0.3328830351, -0.2984357129, 0.1840035673,
 0.1664529435, 2.207054268, 341.6955295, 1.549459936e6 };
// I think, data are from Maple.
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
//FILE *o;o=fopen("fig09c.eps","w"); ado(o,124,82);
// FILE *o;o=fopen("figexcr.eps","w"); ado(o,0,0,126,110);
// FILE *o;o=fopen("sqrt26pl.eps","w"); ado(o,1260,810);
// FILE *o;o=fopen("sqrt26sra.eps","w"); ado(o,660,210);
  FILE *o;o=fopen("sqrt2sra.eps","w"); ado(o,1240,810);
// fprintf(o,"62 12 translate\n 10 10 scale\n");
// fprintf(o,"64 30 translate\n 10 10 scale\n");
// fprintf(o,"620 120 translate\n 100 100 scale\n");
 fprintf(o,"620 110 translate\n 100 100 scale\n");
#define M(x,y) fprintf(o,"%7.4f %7.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%7.4f %7.4f L\n",0.+x,0.+y);
//#define o(x,y) fprintf(o,"%7.4f %7.4f o\n",0.+x,0.+y);

M(0,-1.1)L(0,6.6)
M(-6.1,0)L(6.1,0)
fprintf(o,".03 W S\n");
for(m=-6;m<7;m++){if(m!=0){M(m,-1)L(m,6)}}
for(n=-1;n<7;n++){if(n!=0){M(-6,n)L(6,n)}}
fprintf(o,".01 W S\n");

fprintf(o,"1 setlinejoin 0 setlinecap\n");

for(m=2;m<196;m++){ if(m==2) M(XI[m],.1*DI[m]) else L(XI[m],.1*DI[m]) }
fprintf(o,"1 0 1 RGB S\n");
// No way to see any deviation at this resolution


for(m=0;m<42;m+=1){ x=2.001+.1*m; z=z_type(x,0.);
// d=UQ2L(z); t=Re(d); y=Re(UQ2E(.5+d));
                        d=F43L(z); t=Re(d); y=Re(F43E(.5+d));
                // printf("%6.3f %6.3f %6.3f\n",x,t,y);
                        if(m==0) M(x,y) else L(x,y)}
fprintf(o,".03 W 0 0 1 RGB S\n");

for(m=0;m<104;m+=1){x=3.99-.1*m; z=x;
        // z=TQ2L(z);y=Re(TQ2E(.5+z));
                z=F23L(z);y=Re(F23E(.5+z));
                 if(m/2*2==m) M(x,y) else L(x,y)}
fprintf(o,".06 W 1 0 0 RGB S\n");

DB T4= 19.236149042042854712;
DB T2=-17.143148179354847104;
for(m=0;m<500;m+=1){ x=2.002+.004*m; z=z_type(x,0.);
// c=UQ2L(z); p=Re(UQ2E(.5+c));
// d=TQ2L(z); q=Re(TQ2E(.5+d));
                        c=exq(z); y=1.e24*Re(c);if(m==0) M(x,y) else L(x,y)}
fprintf(o,".005 W 0 .1 0 RGB S\n");

/* NATURAL SEXP
  // solid thin
DO(m,98){x=-6.2+.1*m; z=z_type(x,0.); d=FSLOG(z);y=Re(FSEXP(.5+d)); if(m==0) M(x,y) else L(x,y)}
fprintf(o,".01 W 0 0 0 RGB S\n");
*/

 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
// system( "gv figexcr.eps &"); //for UNIX
// system( "open figexcr.eps"); //for macintosh
        system("epstopdf sqrt2sra.eps");
        system( "open sqrt2sra.pdf"); //for LINUX


//z=3.5;c=exq(z); printf("exq(3.5)=%19.4e %19.4e\n",Re(c),Im(c));
//z=3.;c=exq(z); printf("exq(3.0)=%19.4e %19.4e\n",Re(c),Im(c));
// getchar(); system("killall Preview"); // For macintosh
}

Latex generator of the labels


\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 1230pt
\paperheight 798pt
\topmargin -100pt
\oddsidemargin -75pt
\textwidth 1640pt
\textheight 1600pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document}

%\begin{picture}(360,740)
\begin{picture}(1360,790)
%\put(10,10){\ing{IterPowPlot}}
%\put(40,40){\ing{Itereq2tlo}}
%\put(0,0){\ing{sqrt26plo}}
\put(0,0){\ing{sqrt2sra}}
\put(590,767){\sx{4}{$y$}}
\put(590,697){\sx{4}{$6$}}
\put(590,597){\sx{4}{$5$}}
\put(590,497){\sx{4}{$4$}}
\put(590,396){\sx{4}{$3$}}
\put(590,296){\sx{4}{$2$}}
\put(590,196){\sx{4}{$1$}}
\put(590, 96){\sx{4}{$0$}}
\put(90,50){\sx{4}{$-5$}}
\put(180,50){\sx{4}{$-4$}}
\put(280,50){\sx{4}{$-3$}}
\put(380,50){\sx{4}{$-2$}}
\put(480,50){\sx{4}{$-1$}}
\put(612,50){\sx{4}{$0$}}
\put(712,50){\sx{4}{$1$}}
\put(812,50){\sx{4}{$2$}}
\put(912,50){\sx{4}{$3$}}
\put(1012,50){\sx{4}{$4$}}
\put(1112,50){\sx{4}{$5$}}
\put(1200,50){\sx{4}{$x$}}
\put(778,644){\sx{5}{$y\!=\!\exp_{\sqrt{2},4}^{~ 1/2}(x)$}}
\put(220,150){\sx{5}{$y\!=\!\exp_{\sqrt{2},2}^{~ 1/2}(x)$}}
\put(900,152){\sx{5}{$y\!=\!10^{24}D(x)$}}
\end{picture}
\end{document}

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:14, 1 December 2018Thumbnail for version as of 06:14, 1 December 2018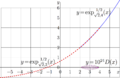2,532 × 1,639 (263 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

The following page uses this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Sqrt2srav.png&oldid=34417"