File:SutrapagT100.jpg
Original file (6,143 × 2,916 pixels, file size: 1.11 MB, MIME type: image/jpeg)
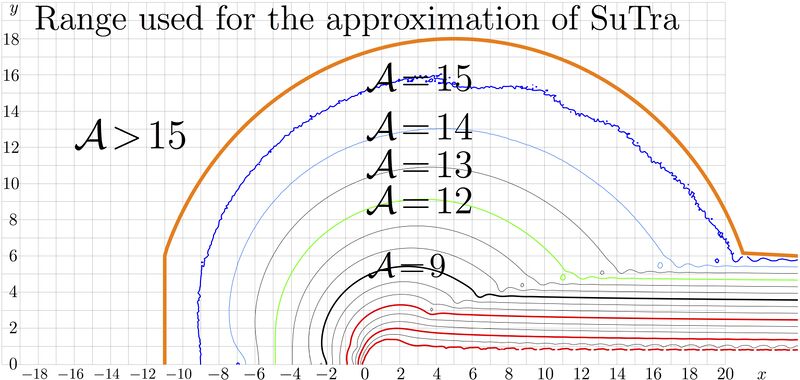
Map of agreement of the primary approximation $\mathrm{Sutra0}_{11}(z)$ for the function SuTra, used in the implementation sutran.cin:
$\displaystyle \mathcal A=\mathcal A(z)=-\lg \left( \frac
Description
SuTra is superfunction of the Trappmann function $\mathrm{tra}(z)=z+\exp(z)$. It is solution of the the transfer equation
$\mathrm{tra}(\mathrm{SuTra}(z))=\mathrm{SuTra}(z\!+\!1)$
with the following asymptotic behaviour:
$\mathrm{SuTra}(z)=\mathrm{SuTra0}_{M}(z)+\mathcal O\left(\frac{\ln(-z)}{z}\right)^{M+1}$
at large positive values of $-\Re(z)$ and/or large $|\Im(z)|$, where $\displaystyle \mathrm{SuTra0}_{M}(z-x_1)=-\ln(-z)+\sum_{m=1}^{M} \frac{\sum_{n=0}^m a_{m,n} \ln(-z)^n}{z^n}$
Constant $a_{1,0}=0$, then, substitution to the Transfer Equation gives $a_{1,1}=-1/2$ and, similarly values of other $a$.
The real constant $~x_1\approx -1.1259817765745026~$ is chosen in such a way to provide the additional condition
$\mathrm{SuTra}(0)=0$
For the plot, value $M=11$ is used; the twelve first terms (since zero to 11) can be calculated exactly with Mathematica software in real time.
The thick orange line indicates the range, used for evaluation of function SuTra . The orange line is formed from the segment of vertical straight line $x=-11$, arc or radius $R=17$ centred at point (5,0), and straight line $y=6$. In the strip along the positive part of the real axis, function $\mathrm{Sutra0}_M$ does not approximate SuTra, and the transfer from the left hand side of the complex planes is used for the evaluation.
Outside the orange loop, the agreement exceeds 15, and the precision of evaluation is limited mainly by the rounding errors of the complex(double) arithmetics; even the line $\mathcal A=14$ already looks a little bit scratched due to the rounding errors. The complex double implementation of function $\mathrm{SuTra}$ is loaded as sutran.cin.
The range of approximation us symmetric with respect to the complex conjugation; so, the only upper half of the complex plane is shown in the picture.
C++ generator of curves
// Files ado.cin, conto.cin and sutran.cin should be loaded to the working directory in order to compile the code below:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include"sutran.cin"
// z_type sutrap(z_type z) { int n; z_type c=sutra0(z-36.); DO(n,36) c=tra(c); return c;}
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//DB x1=-1.1259817765745026; DO(n,8){ y=Re(suzex(x1)); x=y-1.; x1+=-1.2*x; printf("%18.16f %18.16f\n", x1,y);} getchar();
//DB x1=-1.1259817765745026; DO(n,18){ y=Re(sutrap(x1)); x1+=-1.3*y; printf("%18.16f %18.16f\n", x1,y);} getchar();
int M=441,M1=M+1;
int N=201,N1=N+1;
DB X[M1],Y[N1];
DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("SuTraMap.eps","w"); ado(o,4402,2002);
FILE *o;o=fopen("SuTrapag.eps","w"); ado(o,4402,2002);
fprintf(o,"2001 1 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-20+.1*(m-.5);
DO(n,N1) Y[n]=0+.1*(n-.5);
//for(n=0;n<N1;n++) { Y[n]=1.09*sinh((3./200.)*(n-200)); printf("%3d %9.6f\n",n,Y[n]); }
for(m=-20;m<21;m++){M(m,0) L(m,20) }
for(n=0;n<21;n++){M( -20,n) L(20,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999;
f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=sutran(z);
d=sutra0(z);
p=abs(c-d)/(abs(c)+abs(d)); p=-log(p)/log(10.); if(p>0 && p<18) g[m*N1+n]=p;
// p=Re(c); q=Im(c); if(p>-19 && p<19 && ( x<2. || (fabs(q)>1.e-12 && fabs(p)>1.e-12)) ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=1.2;q=.4;
/*
for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-2*p,2*p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
// fprintf(o,"0 setlinejoin 0 setlinecap\n");
// M(-10,0)L(0,0) fprintf(o,"1 1 1 RGB .02 W S\n");
//#include "plofu.cin"
*/
DB angle;
M(24,6)
for(n=20;n<160;n++){ angle=M_PI/180. * n; x=5.+17*cos(angle); y=18*sin(angle); L(x,y)}
L(-11,6) L(-11,0)
fprintf(o,".2 W 1 .5 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (1. ),-2.,2.); fprintf(o,".08 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (2. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (3. ),-2.,2.); fprintf(o,".08 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (4. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (5. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (6. ),-2.,2.); fprintf(o,".08 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (7. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (8. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (9. ),-2.,2.); fprintf(o,".08 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (10. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (11. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (12. ),-2.,2.); fprintf(o,".06 W 0 1 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (13. ),-2.,2.); fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (14. ),-2.,2.); fprintf(o,".03 W 0 .5 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (15. ),-2.,2.); fprintf(o,".06 W 0 0 1 RGB S\n");
//conto(o,g,w,v,X,Y,M,N, (15.4 ),-8.,8.); fprintf(o,".04 W 1 0 1 RGB S\n");
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o); free(f); free(g); free(w);
system("epstopdf sutrapag.eps");
system( "open sutrapag.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of labels
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 4440pt
\paperheight 2108pt
\textwidth 2200pt
\textheight 4500pt
\usepackage {graphics}
\usepackage {rotate}
\newcommand \sx {\scalebox}
\newcommand \ing {\includegraphics}
\topmargin -88pt
\oddsidemargin -80pt
\begin{document}
\begin{picture}(4402,2002)
\put(0,0){\ing{sutrapag}}
\put(44,1955){\sx{8}{$y$}}
\put(04,1775){\sx{8}{$18$}}
\put(04,1575){\sx{8}{$16$}}
\put(04,1375){\sx{8}{$14$}}
\put(04,1175){\sx{8}{$12$}}
\put(04, 975){\sx{8}{$10$}}
\put(040, 775){\sx{8}{$8$}}
\put(040, 575){\sx{8}{$6$}}
\put(040, 375){\sx{8}{$4$}}
\put(040, 175){\sx{8}{$2$}}
%\put(020, 80){\sx{8}{$1$}}
\put(040, -25){\sx{8}{$0$}}
\put(0108,-77){\sx{7}{$-18$}}
\put(0308,-77){\sx{7}{$-16$}}
\put(0508,-77){\sx{7}{$-14$}}
\put(0708,-77){\sx{7}{$-12$}}
\put(0908,-77){\sx{7}{$-10$}}
\put(1140,-80){\sx{8}{$-8$}}
\put(1340,-80){\sx{8}{$-6$}}
\put(1540,-80){\sx{8}{$-4$}}
\put(1740,-80){\sx{8}{$-2$}}
\put(1992,-80){\sx{8}{$0$}}
\put(2192,-80){\sx{8}{$2$}}
\put(2392,-80){\sx{8}{4}}
\put(2592,-80){\sx{8}{6}}
\put(2792,-80){\sx{8}{8}}
\put(2970,-80){\sx{8}{10}}
\put(3170,-80){\sx{8}{12}}
\put(3370,-80){\sx{8}{14}}
\put(3570,-80){\sx{8}{16}}
\put(3770,-80){\sx{8}{18}}
\put(3970,-80){\sx{8}{20}}
\put(4192,-80){\sx{8}{$x$}}
\put(180,1860){\sx{16}{Range used for the approximation of SuTra}}
\put(400,1200){\sx{19}{$\mathcal A \!>\! 15$}}
\put(2020,1520){\sx{18}{$\mathcal A \!=\!15$}}
\put(2020,1250){\sx{18}{$\mathcal A \!=\!14$}}
\put(2020,1040){\sx{18}{$\mathcal A \!=\!13$}}
\put(2020,0840){\sx{18}{$\mathcal A \!=\!12$}}
\put(2030,0488){\sx{16}{$\mathcal A \!=\!9$}}
\end{picture}
\end{document}
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:14, 1 December 2018 |  | 6,143 × 2,916 (1.11 MB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.