File:Tet2uMap.jpg

File
File history
File usage
Metadata

Size of this preview: 800 × 518 pixels. Other resolutions: 320 × 207 pixels | 1,729 × 1,120 pixels.

Original file ‎(1,729 × 1,120 pixels, file size: 526 KB, MIME type: image/jpeg)

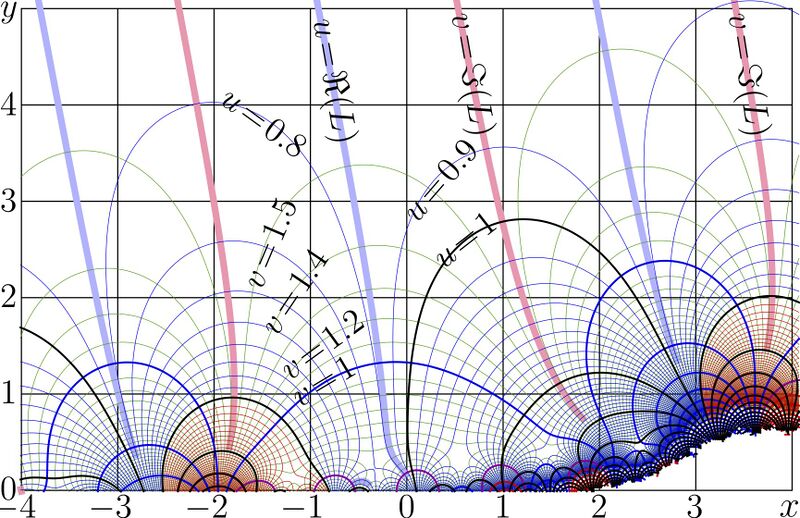
Complex map of Tet2u, approximation of tetration to base 2 for big values of imaginary part of the argument.

C++ generator of map

//Files ado.cin, conto.cin should be loaded in order to compile the code below.//

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
#define z_type std::complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "tet2f4c.cin"
#include "../conto.cin"

z_type L = z_type(0.8246785461420740,1.5674321238496474);
z_type k=log(log(2.)*L);
z_type zK=z_type(1.238069414071370, 1.248161324844940), q=z_type(.1120,-.0150);

//z_type As(z_type z){ z_type c,e;
z_type tet2u(z_type z){ z_type c,e;
e=exp(k*(z-zK));
c=e*(1.
+e*(z_type(-0.1088521804481237,-0.2760741919280730)
+e*(z_type(-0.0494617913252961, 0.0700910465136069)
+e*(z_type( 0.0240455559146310,-0.0029327488470335)
+e*(z_type(-0.0054746528127753,-0.0035758237661136)
+e*(z_type( 0.0005638677469377, 0.0014894502651636)
 ))) )))
;
c+=q*exp(2.*M_PI*I*z)*e;
return c+L;
}

int main(){ int j,k,m,m1,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;

 int M=404,M1=M+1;
 int N=255,N1=N+1;

 DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("tet2uMa.eps","w");ado(o,820,520);
 fprintf(o,"410 10 translate\n 100 100 scale 2 setlinecap\n");
 DO(m,M1)X[m]=-4.01+.02*(m);
 DO(n,N1)Y[n]=-.01+.02*(n);

 for(m=-4;m<5;m++){M(m,-0)L(m,5)}
 for(n=0;n<6;n++){ M( -4,n)L(4,n)}

 fprintf(o,".012 W 0 0 0 RGB S\n");
//M(-2.5,3.5)L(-1.5,3.5)  fprintf(o,".01 W 0 0 0 RGB S\n");
 DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}

 DO(n,N1){y=Y[n];
          for(m=0;m<M1;m++)
          {x=X[m]; //printf("%5.2f\n",x);
           z=z_type(x,y);
        c=tet2u(z);
           p=Re(c);q=Im(c);
           if(p>-99. && p<99. && q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
        }}

 fprintf(o,"1 setlinejoin 2 setlinecap\n"); p=.8;q=.3;

conto(o,f,w,v,X,Y,M,N,1.5674321238496474,-.04, .04); fprintf(o,".07 W 1 .6 .7 RGB S\n");
conto(o,g,w,v,X,Y,M,N,0.8246785461420740,-.04, .04); fprintf(o,".07 W .7 .7 1 RGB S\n");

 for(m=-13;m<16;m++)for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".006 W 0 .6 0 RGB S\n");
 for(m=0;m<16;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".006 W .9 0 0 RGB S\n");
 for(m=0;m<16;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".006 W 0 0 .9 RGB S\n");
 for(m=1;m<16;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".02 W .9 0 0 RGB S\n");
 for(m=1;m<16;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".02 W 0 0 .9 RGB S\n");
                    conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".02 W .6 0 .6 RGB S\n");
 for(m=-17;m<17;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".02 W 0 0 0 RGB S\n");

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf tet2uMa.eps");
//system(   "xpdf  tet2uMa.pdf"); // for Linux
//system( "open tet2ma.pdf"); // for Macintosh
//getchar(); system("killall Preview");
}
//

Latex generator of labels

\documentclass[12pt]{article}
\usepackage{graphicx}
\usepackage{rotating}
\usepackage{geometry}
\paperwidth 830px
\paperheight 538px
\topmargin -108pt
\oddsidemargin -80pt
\pagestyle{empty}
\parindent 0pt
\begin{document}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{picture}(840,530)
%\put(0,6){\includegraphics{figfima}}
%\put(-1,-7){\includegraphics{vladi03a}}
\put(20,10){\includegraphics{tet2uMa}}
\put(8,514){\sx{3}{$y$}}
\put(8,411){\sx{3}{$4$}}
\put(8,311){\sx{3}{$3$}}
\put(8,211){\sx{3}{$2$}}
\put(8,111){\sx{3}{$1$}}
\put(8,11){\sx{3}{$0$}}
\put(0,-8){\sx{3}{$-4$}}
\put(100,-8){\sx{3}{$-3$}}
\put(200,-8){\sx{3}{$-2$}}
\put(300,-8){\sx{3}{$-1$}}
\put(423,-8){\sx{3}{$0$}}
\put(523,-8){\sx{3}{$1$}}
\put(623,-8){\sx{3}{$2$}}
\put(723,-8){\sx{3}{$3$}}
\put(820,-7){\sx{3.2}{$x$}}
\put(334,510){\rot{-80}\sx{3}{$u\!=\!\Re(L)$}\ero}
\put(478,516){\rot{-80}\sx{3}{$v\!=\!\Im(L)$}\ero}
\put(767,516){\rot{-81}\sx{3}{$v\!=\!\Im(L)$}\ero}
\put(236,424){\rot{-36}\sx{3}{$u\!=\!0.8$}\ero}
\put(442,298){\rot{49}\sx{3}{$u\!=\!0.9$}\ero}
\put(470,250){\rot{38}\sx{3}{$u\!=\!1$}\ero}
\put(280,228){\rot{67}\sx{3}{$v\!=\!1.5$}\ero}
\put(296,180){\rot{56}\sx{3}{$v\!=\!1.4$}\ero}
\put(310,134){\rot{36}\sx{3}{$v\!=\!1.2$}\ero}
\put(320,106){\rot{31}\sx{3}{$v\!=\!1$}\ero}
\end{picture}
\end{document}

Description

This map is not included to Book Superfunctions, because that Book becomes too thick and difficult to handle.

The complex double implementation of function Tet2u returns 15 correct decimal figures.

The Kneser expansion is used for the implementation.

The following approximation for the Kneser parameter is used:

\( z_{\mathrm K}=1.23806941407137 + 1.24816132484494 \, \mathrm i \)

One term of the second Kneser series is added with coefficient \( q= 0.112 -0.015 \, \mathrm i \)

Function tet2u approximates tet2\((z)\), id est, tetration to base 2 for small values of

\( \varepsilon = \exp(k (z\!-\! z_{\mathrm K})) \)

where \(k\) is increment of the exponential approximation of the tetration. Parameters of that approximation are evaluated with the code below; file filog.cin should be loaded for the compiling.

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
#define z_type std::complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)

#include"Filog.cin"

int main(){ FILE *o;
o=fopen("fco.cin","w");
z_type b=2.;
fprintf(o,"/%s base b=2; fco.cin is beow:\n","/");

z_type L=Filog(log(b));
fprintf(o,"z_type L=z_type(%19.16lf,%19.16lf);\n",Re(L),Im(L));

//test:
z_type L1=exp(log(b)*L);
z_type L2=log(L)/log(b);
printf("Test of L\n");
printf("L0: %19.16lf %19.16lf\n", Re(L),Im(L));
printf("L1: %19.16lf %19.16lf\n", Re(L1),Im(L1));
printf("L2: %19.16lf %19.16lf\n", Re(L2),Im(L2));

z_type s=log(L);
fprintf(o,"z_type s=z_type(%19.16lf,%19.16lf);\n",Re(s),Im(s));

z_type k=log(s);
fprintf(o,"z_type k=z_type(%19.16lf,%19.16lf);\n",Re(k),Im(k));
 
z_type P=2.*M_PI*I/k;
fprintf(o,"z_type P=z_type(%19.16lf,%19.16lf);\n",Re(P),Im(P));
 
fprintf(o,"/%s This is for fima; f(z)=Sum c_n epsilon^n. Do not confuse with gco.cin \n","/");

fprintf(o,"z_type c[7]={\n");

fprintf(o,"z_type(%19.16lf,%19.16lf), 1.,\n", Re(L),Im(L)); // 0th and 1st coefficients are here!

z_type s1=1.-s;
z_type p2=s/(L*s1);
z_type c2=-.5*p2;
fprintf(o,"z_type(%19.16lf,%19.16lf),\n", Re(c2),Im(c2));

z_type s2=1.-s*s;
z_type p3=p2*s/(L*s2);
z_type c3=p3*(2.+s)/6.;
fprintf(o,"z_type(%19.16lf,%19.16lf),\n", Re(c3),Im(c3));

z_type s3=1.-s*s*s;
z_type p4=p3*s/(L*s3);
z_type c4=-p4*(
6.+s*(6.+s*(5.+s))
)/24.;
fprintf(o,"z_type(%19.16lf,%19.16lf),\n", Re(c4),Im(c4));

z_type s4=1.-s*s*s*s;
z_type p5=p4*s/(L*s4);
z_type c5=p5*(
24.+s*(36.+s*(46.+s*(40.+s*(24.+s*(9.+s))) ))
)/120.;
fprintf(o,"z_type(%19.16lf,%19.16lf),\n", Re(c5),Im(c5));

z_type s5=1.-s*s*s*s*s;
z_type p6=p5*s/(L*s5);
z_type c6=-p6*(
120.+s*(240.+s*(390.+s*(480.+s*(514.+s*(416.+s*(301.+s*(160.+s*(64.+s
*(14.+s))))) ))))
)/720.;

fprintf(o,"z_type(%19.16lf,%19.16lf)\n", Re(c6),Im(c6));

fprintf(o,"};\n");

fclose(o);
system("more fco.cin");
}

The output file fco.cin is:

// base b=2; fco.cin is beow:
z_type L=z_type( 0.8246785461420740, 1.5674321238496474);
z_type s=z_type( 0.5716236091266532, 1.0864611573654703);
z_type k=z_type( 0.2051106885449890, 1.0864611573654706);
z_type P=z_type( 5.5841424355433897, 1.0542183603369362);
// This is for fima; f(z)=Sum c_n epsilon^n. Do not confuse with gco.cin 
z_type c[7]={
z_type( 0.8246785461420740, 1.5674321238496474), 1.,
z_type(-0.1088521804481237,-0.2760741919280730),
z_type(-0.0494617913252961, 0.0700910465136069),
z_type( 0.0240455559146310,-0.0029327488470335),
z_type(-0.0054746528127753,-0.0035758237661136),
z_type( 0.0005638677469377, 0.0014894502651636)
};

Coefficient of the expansion are described in book Superfunctions: page 63, eq.(6.2)-(6.11) ^[1]; in the Russian version: page 70, eq.(6.5) - (6.10) ^[2].

For tetration to arbitrary base, the coefficients of the expansion are calculated by Wiliam Paulsen and Samuel Cowgill ^[3]^[4].

In order to break the translational symmetry of the approximation (and simplify the evaluation of the Kneser parameter), one term of the second Kneser series is added with empiric coefficient.

References

↑ https://mizugadro.mydns.jp/BOOK/465.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020, in press.
↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 Дмитрий Кузнецов. Суперфункции. Нецелые итерации голоморфных функций. Тетрация и другие суперфункции. Формулы, алгоритмы, графики и комплексные карты. Lambert Academic Publishing, 2014.
↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving \(F(z+1) = b^{F(z)}\) in the complex plane. Advances in Computational Mathematics volume 43, pages 1261-1282 (2017)
↑ https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics volume 45, pages 243-267 (2019)

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	22:34, 23 July 2020		1,729 × 1,120 (526 KB)	T (talk \| contribs)

You cannot overwrite this file.

File usage

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	150 dpi
Vertical resolution	150 dpi

[1] ttps://mizugadro.mydns.jp/BOOK/465.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020, in press.

[2] ttps://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 Дмитрий Кузнецов. Суперфункции. Нецелые итерации голоморфных функций. Тетрация и другие суперфункции. Формулы, алгоритмы, графики и комплексные карты. Lambert Academic Publishing, 2014.

[3] ttps://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving \(F(z+1) = b^{F(z)}\) in the complex plane. Advances in Computational Mathematics volume 43, pages 1261-1282 (2017)

[4] ttps://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics volume 45, pages 243-267 (2019)

[1]

[2]

[3]

[4]