Difference between revisions of "File:Sqrt2q2map600.jpg"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
 
Line 1: Line 1:
  +
[[Complex map]] of the half iterate of exponent to base $\sqrt{2}$ regular at its lowest fixed point.
−
Importing image file
  
  +
  +
$u\!+\!\mathrm i v= \exp_{\sqrt{2},\mathrm d}^{~ 1/2}(x\!+\!\mathrm i y)$
  +
  +
This function is expressed through [[tetration]] and [[arctetration]] to base $\sqrt{2}$:
  +
  +
$\displaystyle
  +
\exp_{\sqrt{2},\mathrm d}^{~ 1/2}(z)= \mathrm{tet}_{\sqrt{2}}\left( \frac{1}{2}+\mathrm{ate}_{\sqrt{2}}(z) \right)$
  +
  +
Usage: this is figure 16.8 of the book [[Суперфункции]] (2014, In Russian) <ref>
  +
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
  +
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br>
  +
http://mizugadro.mydns.jp/BOOK/202.pdf
  +
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014.
  +
</ref>; the English version is in preparation in 2015.
  +
  +
The same map appears also at the top left picture of figure 6 of article
  +
<ref>
  +
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br>
  +
http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint
  +
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
  +
</ref>.
  +
  +
  +
==Refereces==
  +
<references/>
  +
  +
==[[C++]] generator of the map==
  +
Files [[ado.cin]], [[conto.cin]], and
  +
  +
[[sqrt2f21e.cin]],
  +
[[sqrt2f21l.cin]],
  +
  +
or
  +
  +
[[sqrt2f23e.cin]],
  +
[[sqrt2f23l.cin]]
  +
  +
should be loaded in order to compile the code below.
  +
<poem><nomathjax><nowiki>
  +
  +
#include <math.h>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
#include <complex>
  +
typedef std::complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
#include "conto.cin"
  +
  +
// #include "uq2e.cin"
  +
// #include "uq2L.cin"
  +
// #include "f43E.cin"
  +
// #include "f43L.cin"
  +
//#include "sqrt2f23e.cin"
  +
//#include "sqrt2f23l.cin"
  +
#include "sqrt2f21e.cin"
  +
#include "sqrt2f21l.cin"
  +
  +
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
  +
int M=211,M1=M+1;
  +
int N=201,N1=N+1;
  +
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
  +
char v[M1*N1]; // v is working array
  +
FILE *o;o=fopen("sqrt26a.eps","w"); ado(o,214,212);
  +
fprintf(o,"112 110 translate\n 10 10 scale\n");
  +
DO(m,M1) X[m]=-11+.1*(m-.5);
  +
DO(n,N1) Y[n]=-10+.1*(n-.5);
  +
for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
  +
for(n=-10;n<11;n++) {M( -10,n)L(10,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
  +
  +
//fprintf(o,"/adobe-Roman findfont 1 scalefont setfont\n");
  +
// for(m=-8;m<0;m+=2) {M(-11.2,m-.3) fprintf(o,"(%1d)s\n",m);}
  +
// for(m= 0;m<9;m+=2) {M(-10.7,m-.3) fprintf(o,"(%1d)s\n",m);}
  +
// for(m=-8;m<0;m+=4) {M(m-.6,-10.8) fprintf(o,"(%1d)s\n",m);}
  +
// for(m= 0;m<9;m+=4) {M(m-.3,-10.8) fprintf(o,"(%1d)s\n",m);}
  +
  +
// fprintf(o,"/Times-Italic findfont 1 scalefont setfont\n");
  +
//fprintf(o,"/adobe-italic findfont 1 scalefont setfont\n");
  +
// M(-10.7, 9.5) fprintf(o,"(y)s\n");
  +
// M( 9.6,-10.8) fprintf(o,"(x)s\n");
  +
// M(-11,0)L(10.1,0) M(0,-11)L(0,10.1) fprintf(o,".01 W 1 0 1 RGB S\n");
  +
// z_type tm,tp,F[M1*N1];;
  +
DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
  +
f[m*N1+n]=9999;}
  +
DO(m,M1){x=X[m];
  +
DO(n,N1){y=Y[n]; z=z_type(x,y);
  +
if(abs(z-10.)>2.9)
  +
{
  +
// c=UQ2E(z) ; d=uq2LA(c);
  +
// c=UQ2L(z); c=UQ2E(c+.5);
  +
// c=F43L(z); c=F43E(c+.5);
  +
c=F23L(z); c=F23E(c+.5);
  +
// p=abs((z-d)/(z+d)); p=-log(p)/log(10.);
  +
p=Re(c); q=Im(c);
  +
if(p>-99 && p<99 && fabs(p)>1.e-12) g[m*N1+n]=p;
  +
if(q>-99 && q<99 && fabs(q)>1.e-12) f[m*N1+n]=q;
  +
}}}
  +
p=2; q=1;
  +
#include "plofu.cin"
  +
  +
// p=1.e-15;
  +
//for(n=-10;n<11;n++) {q=p*n; z=z_type(q,0.); printf("%19.15f %19.16f\n",q, Re(uq2e(z)) ); }
  +
//M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");
  +
  +
/*
  +
y=9.064720284;
  +
M(.89, y)L(10.1, y)
  +
M(.89,-y)L(10.1,-y)
  +
M(4,0)L( 10,0)fprintf(o,".15 W 0 0 0 RGB [.2 .2] 0 setdash S\n");
  +
*/
  +
//The cuts live in a separate file, but one will be more stressed:
  +
M(4,0)L( 10.1,0)
  +
fprintf(o,".1 W 1 1 1 RGB S\n");
  +
DO(n,28){M(4+.3*n,0)L(4+.3*(n+.5),0)} fprintf(o,".13 W 0 0 0 RGB S\n");
  +
  +
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
  +
system("epstopdf sqrt26a.eps");
  +
system( "open sqrt26a.pdf"); // for LINUX
  +
// getchar(); system("killall Preview"); // For macintosh
  +
}
  +
  +
</nowiki></nomathjax></poem>
  +
  +
==[[C++]] generator of the cut lines==
  +
Files [[ado.cin]],
  +
[[sqrt2f21e.cin]],
  +
[[sqrt2f21l.cin]]
  +
should be loaded in order to compile the code below.
  +
<poem><nomathjax><nowiki>
  +
  +
#include <math.h>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
#include <complex>
  +
typedef std::complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
#include "conto.cin"
  +
  +
// #include "uq2e.cin"
  +
// #include "uq2L.cin"
  +
// #include "f43E.cin"
  +
// #include "f43L.cin"
  +
  +
// #include "f23E.cin"
  +
#include "sqrt2f21L.cin"
  +
  +
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
  +
int M= 60,M1=M+1;
  +
int N=201,N1=N+1;
  +
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
  +
char v[M1*N1]; // v is working array
  +
FILE *o;o=fopen("sqrt26cuts.eps","w"); ado(o,214,212);
  +
fprintf(o,"112 110 translate\n 10 10 scale\n");
  +
DO(m,M1) X[m]= 4.2 +.1*(m-.5);
  +
DO(n,N1) Y[n]=-10+.1*(n-.5);
  +
for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
  +
for(n=-10;n<11;n++) {M( -10,n)L(10,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
  +
// fprintf(o,"/adobe-Roman findfont 1 scalefont setfont\n");
  +
// for(m=-8;m<0;m+=2) {M(-11.2,m-.3) fprintf(o,"(%1d)s\n",m);}
  +
// for(m= 0;m<9;m+=2) {M(-10.7,m-.3) fprintf(o,"(%1d)s\n",m);}
  +
// for(m=-8;m<0;m+=4) {M(m-.6,-10.8) fprintf(o,"(%1d)s\n",m);}
  +
// for(m= 0;m<9;m+=4) {M(m-.3,-10.8) fprintf(o,"(%1d)s\n",m);}
  +
// fprintf(o,"/Times-Italic findfont 1 scalefont setfont\n");
  +
// //fprintf(o,"/adobe-italic findfont 1 scalefont setfont\n");
  +
// M(-10.7, 9.5) fprintf(o,"(y)s\n");
  +
// M( 9.6,-10.8) fprintf(o,"(x)s\n");
  +
// M(-11,0)L(10.1,0) M(0,-11)L(0,10.1) fprintf(o,".01 W 1 0 1 RGB S\n");
  +
// z_type tm,tp,F[M1*N1];;
  +
DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
  +
f[m*N1+n]=9999;}
  +
DO(m,M1){x=X[m];
  +
DO(n,N1){y=Y[n];
  +
if(fabs(fabs(y)-9.)>.3)
  +
{ z=z_type(x,y);
  +
c=F21L(z);
  +
p=Re(c); q=Im(c);
  +
if(p>-99 && p<99) g[m*N1+n]=p;
  +
if(q>-99 && q<99 && fabs(q)>1.e-12) f[m*N1+n]=q;
  +
}}}
  +
//#include "plofu.cin"
  +
  +
conto(o,f,w,v,X,Y,M,N, (0. ), -2,2); // fprintf(o,".05 W 0 .8 0 RGB S\n");
  +
  +
/*
  +
y=9.064720284;
  +
M(.89, y)L(10.1, y)
  +
M(.89,-y)L(10.1,-y)
  +
M(4,0)L( 10,0)
  +
*/
  +
  +
// fprintf(o,".1 W 0 0 0 RGB [.2 .2] 0 setdash S\n");
  +
  +
y=9.064720284;
  +
M(.89, y)L(10.1, y)
  +
M(.89,-y)L(10.1,-y)
  +
M(4,0)L( 10,0)fprintf(o,".07 W 0 0 0 RGB [.2 .2] 0 setdash S\n");
  +
  +
fprintf(o,"[99]0 setdash\n");
  +
  +
/*
  +
M(2,0)L(-11.2,0)fprintf(o,".1 W 1 1 1 RGB S\n");
  +
DO(n,36){M(2-.3*n,0)L(2-.3*(n+.5),0)} fprintf(o,".15 W 0 0 0 RGB S\n");
  +
//M(2,0)L(-11,0)fprintf(o,".15 W 0 0 0 RGB [.2 .2] 0 setdash S\n"); //may cause problems
  +
*/
  +
  +
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
  +
system("epstopdf sqrt26cuts.eps");
  +
system( "open sqrt26cuts.pdf");
  +
// getchar(); system("killall Preview"); // For macintosh
  +
}
  +
</nowiki></nomathjax></poem>
  +
  +
==[[Latex]] combiner==
  +
  +
<poem><nomathjax><nowiki>
  +
\documentclass[12pt]{article}
  +
\paperwidth 212px
  +
\paperheight 210px
  +
\textwidth 1394px
  +
\textheight 1300px
  +
\topmargin -100px
  +
\oddsidemargin -74px
  +
\usepackage{graphics}
  +
\usepackage{rotating}
  +
\newcommand \sx {\scalebox}
  +
\newcommand \rot {\begin{rotate}}
  +
\newcommand \ero {\end{rotate}}
  +
\newcommand \ing {\includegraphics}
  +
\newcommand \rmi {\mathrm{i}}
  +
\parindent 0pt
  +
\pagestyle{empty}
  +
\begin{document}\parindent 0pt
  +
  +
\sx{1.}{\begin{picture}(280,203)
  +
%\put(0,0){\ing{exc2cuts}}
  +
%\put(0,0){\ing{figexc2}}
  +
\put(0,0){\ing{sqrt26cuts}}
  +
\put(0,0){\ing{sqrt26a}}
  +
\put(6,207.7){\sx{.7}{$y$}}
  +
\put(6,187.8){\sx{.7}{$8$}}
  +
\put(6,167.8){\sx{.7}{$6$}}
  +
\put(6,147.7){\sx{.7}{$4$}}
  +
\put(6,127.7){\sx{.7}{$2$}}
  +
\put(6,107.7){\sx{.7}{$0$}}
  +
\put(0, 87.7){\sx{.7}{$-2$}}
  +
\put(0, 67.6){\sx{.7}{$-4$}}
  +
\put(0, 47.6){\sx{.7}{$-6$}}
  +
\put(0, 27.5){\sx{.7}{$-8$}}
  +
\put(3, 2){\sx{.7}{$-10$}}
  +
\put( 27,2){\sx{.7}{$-8$}}
  +
\put( 47,2){\sx{.7}{$-6$}}
  +
\put( 67,2){\sx{.7}{$-4$}}
  +
\put( 87,2){\sx{.7}{$-2$}}
  +
\put(111,2){\sx{.7}{$0$}}
  +
\put(131,2){\sx{.7}{$2$}}
  +
\put(151,2){\sx{.7}{$4$}}
  +
\put(171,2){\sx{.7}{$6$}}
  +
\put(191,2){\sx{.7}{$8$}}
  +
\put(210,2){\sx{.7}{$x$}}
  +
%\put( 27,127){\sx{3}{$\exp_{b,2}^{[1/2]}$}}
  +
\put(23,198.6){\sx{.9}{$v\!=\!0$}}
  +
\put(33.7,92){\rot{90}\sx{.9}{$u\!=\!-1.2$}\ero}
  +
\put(59.6,96){\rot{90}\sx{.9}{$u\!=\!-1$}\ero}
  +
\put(102,98){\rot{90}\sx{.9}{$u\!=\!0$}\ero}
  +
\put(122,99){\rot{90}\sx{.9}{$u\!=\!1$}\ero}
  +
\put(136,99){\rot{90}\sx{.9}{$u\!=\!2$}\ero}
  +
%\put(215,207){\sx{.8}{\bf cut}}
  +
\put(195,199){\sx{.8}{\bf cut}}
  +
\put(197,184){\rot{24}{\sx{.78}{\bf cut}}\ero}
  +
\put(204.4,174.4){\rot{40}{\sx{.78}{\bf cut}}\ero}
  +
%\put(215,184){\sx{.8}{\bf cut}}
  +
%\put(215,175){\sx{.8}{\bf cut}}
  +
\put(195,108){\sx{.78}{\bf cut}}
  +
%
  +
\put(87,145){\rot{-44}\sx{.9}{$v\!=\!1$}\ero}
  +
\put(61,122){\rot{-15}\sx{.8}{$v\!=\!0.2$}\ero}
  +
\put(63,108){\sx{.9}{$v\!=\!0$}}
  +
\put(62, 94){\rot{13}\sx{.8}{$v\!=\!-0.2$}\ero}
  +
%\put(215, 42){\sx{.8}{\bf cut}}
  +
%\put(215, 33){\sx{.8}{\bf cut}}
  +
%\put(215, 25){\sx{.8}{\bf cut}}
  +
\put(196,32){\rot{-22}{\sx{.78}{\bf cut}}\ero}
  +
\put(195, 17){\sx{.78}{\bf cut}}
  +
%\put(-23, 17){\sx{1.}{$q\!=0$}}
  +
%\put(215, 10){\sx{.8}{\bf cut}}
  +
\put(23,17){\sx{.9}{$v\!=\!0$}}
  +
\end{picture}}
  +
  +
\end{document}
  +
</nowiki></nomathjax></poem>
  +
  +
  +
[[Category:Base sqrt2]]
  +
[[Category:Sqrt2]]
  +
[[Category:Book]]
  +
[[Category:BookMap]]
  +
[[Category:C++]]
  +
[[Category:Complex map]]
  +
[[Category:Exp]]
  +
[[Category:Generator]]
  +
[[Category:Latex]]
  +
[[Category:Superfunction]]
  +
[[Category:Tetration]]

Latest revision as of 08:52, 1 December 2018

Complex map of the half iterate of exponent to base $\sqrt{2}$ regular at its lowest fixed point.

$u\!+\!\mathrm i v= \exp_{\sqrt{2},\mathrm d}^{~ 1/2}(x\!+\!\mathrm i y)$

This function is expressed through tetration and arctetration to base $\sqrt{2}$:

$\displaystyle \exp_{\sqrt{2},\mathrm d}^{~ 1/2}(z)= \mathrm{tet}_{\sqrt{2}}\left( \frac{1}{2}+\mathrm{ate}_{\sqrt{2}}(z) \right)$

Usage: this is figure 16.8 of the book Суперфункции (2014, In Russian) [1]; the English version is in preparation in 2015.

The same map appears also at the top left picture of figure 6 of article [2].


Refereces

  1. ↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
    http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
    http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.
  2. ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
    http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.

C++ generator of the map

Files ado.cin, conto.cin, and

sqrt2f21e.cin, sqrt2f21l.cin,

or

sqrt2f23e.cin, sqrt2f23l.cin

should be loaded in order to compile the code below.



#include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"

// #include "uq2e.cin"
// #include "uq2L.cin"
// #include "f43E.cin"
// #include "f43L.cin"
//#include "sqrt2f23e.cin"
//#include "sqrt2f23l.cin"
 #include "sqrt2f21e.cin"
 #include "sqrt2f21l.cin"

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
 int M=211,M1=M+1;
 int N=201,N1=N+1;
 DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("sqrt26a.eps","w"); ado(o,214,212);
 fprintf(o,"112 110 translate\n 10 10 scale\n");
 DO(m,M1) X[m]=-11+.1*(m-.5);
 DO(n,N1) Y[n]=-10+.1*(n-.5);
 for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
 for(n=-10;n<11;n++) {M( -10,n)L(10,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
 
//fprintf(o,"/adobe-Roman findfont 1 scalefont setfont\n");
// for(m=-8;m<0;m+=2) {M(-11.2,m-.3) fprintf(o,"(%1d)s\n",m);}
// for(m= 0;m<9;m+=2) {M(-10.7,m-.3) fprintf(o,"(%1d)s\n",m);}
// for(m=-8;m<0;m+=4) {M(m-.6,-10.8) fprintf(o,"(%1d)s\n",m);}
// for(m= 0;m<9;m+=4) {M(m-.3,-10.8) fprintf(o,"(%1d)s\n",m);}

// fprintf(o,"/Times-Italic findfont 1 scalefont setfont\n");
 //fprintf(o,"/adobe-italic findfont 1 scalefont setfont\n");
// M(-10.7, 9.5) fprintf(o,"(y)s\n");
// M( 9.6,-10.8) fprintf(o,"(x)s\n");
// M(-11,0)L(10.1,0) M(0,-11)L(0,10.1) fprintf(o,".01 W 1 0 1 RGB S\n");
// z_type tm,tp,F[M1*N1];;
 DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
                        f[m*N1+n]=9999;}
 DO(m,M1){x=X[m];
 DO(n,N1){y=Y[n]; z=z_type(x,y);
          if(abs(z-10.)>2.9)
        {
 // c=UQ2E(z) ; d=uq2LA(c);
 // c=UQ2L(z); c=UQ2E(c+.5);
 // c=F43L(z); c=F43E(c+.5);
        c=F23L(z); c=F23E(c+.5);
  // p=abs((z-d)/(z+d)); p=-log(p)/log(10.);
        p=Re(c); q=Im(c);
        if(p>-99 && p<99 && fabs(p)>1.e-12) g[m*N1+n]=p;
        if(q>-99 && q<99 && fabs(q)>1.e-12) f[m*N1+n]=q;
        }}}
p=2; q=1;
#include "plofu.cin"

// p=1.e-15;
//for(n=-10;n<11;n++) {q=p*n; z=z_type(q,0.); printf("%19.15f %19.16f\n",q, Re(uq2e(z)) ); }
//M(-10,0)L(-2,0)fprintf(o,".04 W 1 0 1 RGB S\n");

/*
y=9.064720284;
M(.89, y)L(10.1, y)
M(.89,-y)L(10.1,-y)
M(4,0)L( 10,0)fprintf(o,".15 W 0 0 0 RGB [.2 .2] 0 setdash S\n");
*/
//The cuts live in a separate file, but one will be more stressed:
M(4,0)L( 10.1,0)
fprintf(o,".1 W 1 1 1 RGB S\n");
DO(n,28){M(4+.3*n,0)L(4+.3*(n+.5),0)} fprintf(o,".13 W 0 0 0 RGB S\n");

 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
        system("epstopdf sqrt26a.eps");
        system( "open sqrt26a.pdf"); // for LINUX
// getchar(); system("killall Preview"); // For macintosh
}

C++ generator of the cut lines

Files ado.cin, sqrt2f21e.cin, sqrt2f21l.cin should be loaded in order to compile the code below.



 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"

// #include "uq2e.cin"
// #include "uq2L.cin"
// #include "f43E.cin"
// #include "f43L.cin"

// #include "f23E.cin"
 #include "sqrt2f21L.cin"

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
 int M= 60,M1=M+1;
 int N=201,N1=N+1;
 DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
 char v[M1*N1]; // v is working array
 FILE *o;o=fopen("sqrt26cuts.eps","w"); ado(o,214,212);
 fprintf(o,"112 110 translate\n 10 10 scale\n");
 DO(m,M1) X[m]= 4.2 +.1*(m-.5);
 DO(n,N1) Y[n]=-10+.1*(n-.5);
 for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
 for(n=-10;n<11;n++) {M( -10,n)L(10,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
// fprintf(o,"/adobe-Roman findfont 1 scalefont setfont\n");
// for(m=-8;m<0;m+=2) {M(-11.2,m-.3) fprintf(o,"(%1d)s\n",m);}
// for(m= 0;m<9;m+=2) {M(-10.7,m-.3) fprintf(o,"(%1d)s\n",m);}
// for(m=-8;m<0;m+=4) {M(m-.6,-10.8) fprintf(o,"(%1d)s\n",m);}
// for(m= 0;m<9;m+=4) {M(m-.3,-10.8) fprintf(o,"(%1d)s\n",m);}
// fprintf(o,"/Times-Italic findfont 1 scalefont setfont\n");
// //fprintf(o,"/adobe-italic findfont 1 scalefont setfont\n");
// M(-10.7, 9.5) fprintf(o,"(y)s\n");
// M( 9.6,-10.8) fprintf(o,"(x)s\n");
// M(-11,0)L(10.1,0) M(0,-11)L(0,10.1) fprintf(o,".01 W 1 0 1 RGB S\n");
// z_type tm,tp,F[M1*N1];;
 DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
                        f[m*N1+n]=9999;}
 DO(m,M1){x=X[m];
 DO(n,N1){y=Y[n];
        if(fabs(fabs(y)-9.)>.3)
        { z=z_type(x,y);
        c=F21L(z);
        p=Re(c); q=Im(c);
        if(p>-99 && p<99) g[m*N1+n]=p;
        if(q>-99 && q<99 && fabs(q)>1.e-12) f[m*N1+n]=q;
        }}}
//#include "plofu.cin"

conto(o,f,w,v,X,Y,M,N, (0. ), -2,2); // fprintf(o,".05 W 0 .8 0 RGB S\n");

/*
y=9.064720284;
M(.89, y)L(10.1, y)
M(.89,-y)L(10.1,-y)
M(4,0)L( 10,0)
*/

// fprintf(o,".1 W 0 0 0 RGB [.2 .2] 0 setdash S\n");

y=9.064720284;
M(.89, y)L(10.1, y)
M(.89,-y)L(10.1,-y)
M(4,0)L( 10,0)fprintf(o,".07 W 0 0 0 RGB [.2 .2] 0 setdash S\n");

fprintf(o,"[99]0 setdash\n");

/*
M(2,0)L(-11.2,0)fprintf(o,".1 W 1 1 1 RGB S\n");
DO(n,36){M(2-.3*n,0)L(2-.3*(n+.5),0)} fprintf(o,".15 W 0 0 0 RGB S\n");
//M(2,0)L(-11,0)fprintf(o,".15 W 0 0 0 RGB [.2 .2] 0 setdash S\n"); //may cause problems
*/

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
        system("epstopdf sqrt26cuts.eps");
        system( "open sqrt26cuts.pdf");
// getchar(); system("killall Preview"); // For macintosh
}

Latex combiner


\documentclass[12pt]{article}
\paperwidth 212px
\paperheight 210px
\textwidth 1394px
\textheight 1300px
\topmargin -100px
\oddsidemargin -74px
\usepackage{graphics}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \rmi {\mathrm{i}}
\parindent 0pt
\pagestyle{empty}
\begin{document}\parindent 0pt

\sx{1.}{\begin{picture}(280,203)
%\put(0,0){\ing{exc2cuts}}
%\put(0,0){\ing{figexc2}}
\put(0,0){\ing{sqrt26cuts}}
\put(0,0){\ing{sqrt26a}}
\put(6,207.7){\sx{.7}{$y$}}
\put(6,187.8){\sx{.7}{$8$}}
\put(6,167.8){\sx{.7}{$6$}}
\put(6,147.7){\sx{.7}{$4$}}
\put(6,127.7){\sx{.7}{$2$}}
\put(6,107.7){\sx{.7}{$0$}}
\put(0, 87.7){\sx{.7}{$-2$}}
\put(0, 67.6){\sx{.7}{$-4$}}
\put(0, 47.6){\sx{.7}{$-6$}}
\put(0, 27.5){\sx{.7}{$-8$}}
\put(3, 2){\sx{.7}{$-10$}}
\put( 27,2){\sx{.7}{$-8$}}
\put( 47,2){\sx{.7}{$-6$}}
\put( 67,2){\sx{.7}{$-4$}}
\put( 87,2){\sx{.7}{$-2$}}
\put(111,2){\sx{.7}{$0$}}
\put(131,2){\sx{.7}{$2$}}
\put(151,2){\sx{.7}{$4$}}
\put(171,2){\sx{.7}{$6$}}
\put(191,2){\sx{.7}{$8$}}
\put(210,2){\sx{.7}{$x$}}
%\put( 27,127){\sx{3}{$\exp_{b,2}^{[1/2]}$}}
\put(23,198.6){\sx{.9}{$v\!=\!0$}}
\put(33.7,92){\rot{90}\sx{.9}{$u\!=\!-1.2$}\ero}
\put(59.6,96){\rot{90}\sx{.9}{$u\!=\!-1$}\ero}
\put(102,98){\rot{90}\sx{.9}{$u\!=\!0$}\ero}
\put(122,99){\rot{90}\sx{.9}{$u\!=\!1$}\ero}
\put(136,99){\rot{90}\sx{.9}{$u\!=\!2$}\ero}
%\put(215,207){\sx{.8}{\bf cut}}
\put(195,199){\sx{.8}{\bf cut}}
\put(197,184){\rot{24}{\sx{.78}{\bf cut}}\ero}
\put(204.4,174.4){\rot{40}{\sx{.78}{\bf cut}}\ero}
%\put(215,184){\sx{.8}{\bf cut}}
%\put(215,175){\sx{.8}{\bf cut}}
\put(195,108){\sx{.78}{\bf cut}}
%
\put(87,145){\rot{-44}\sx{.9}{$v\!=\!1$}\ero}
\put(61,122){\rot{-15}\sx{.8}{$v\!=\!0.2$}\ero}
\put(63,108){\sx{.9}{$v\!=\!0$}}
\put(62, 94){\rot{13}\sx{.8}{$v\!=\!-0.2$}\ero}
%\put(215, 42){\sx{.8}{\bf cut}}
%\put(215, 33){\sx{.8}{\bf cut}}
%\put(215, 25){\sx{.8}{\bf cut}}
\put(196,32){\rot{-22}{\sx{.78}{\bf cut}}\ero}
\put(195, 17){\sx{.78}{\bf cut}}
%\put(-23, 17){\sx{1.}{$q\!=0$}}
%\put(215, 10){\sx{.8}{\bf cut}}
\put(23,17){\sx{.9}{$v\!=\!0$}}
\end{picture}}

\end{document}

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:14, 1 December 2018Thumbnail for version as of 06:14, 1 December 2018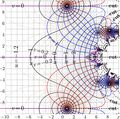1,766 × 1,750 (1.43 MB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Sqrt2q2map600.jpg&oldid=21604"