Difference between revisions of "File:TraplotT.jpg"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
  +
[[Explicit plot]] of the [[Trappmann function]]
−
Importing image file
  
  +
  +
$y=\mathrm{tra}(x)=\exp(x)\!+\!x$
  +
  +
For comparison, the [[exponent]] is shown,
  +
  +
$y=\exp(x)$
  +
  +
This function is interesting as a [[transfer function]], because it has no [[fixed point]].
  +
One of its [[superfunction]]s, namely, [[SuTra]], is entire function with logarithmic asymptotic
  +
<ref>
  +
http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541
  +
</ref>.
  +
  +
The image is used as Figure 20.1 in book [[Superfunction]] (In Russian, 2014; the English version is in preparation, 2015)
  +
<ref>
  +
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
  +
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br>
  +
http://mizugadro.mydns.jp/BOOK/202.pdf
  +
Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
  +
</ref>.
  +
  +
==References==
  +
<references/>
  +
  +
==[[C++]] generator of curves==
  +
  +
Files [[ado.cin]], should be loaded to the working directory in order to compile the code below
  +
<poem><nomathjax><nowiki>
  +
#include <math.h>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
//using namespace std;
  +
#include<complex>
  +
typedef std::complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
//#include "Tania.cin" // need for LambertW
  +
/*
  +
#include "doya.cin" // need for LambertW
  +
#include "LambertW.cin" // need for AuZex
  +
#include "SuZex.cin"
  +
#include "AuZex.cin"
  +
*/
  +
z_type tra(z_type z){ return exp(z)+z;}
  +
/*
  +
z_type F(z_type z){ return log(suzex(z));}
  +
z_type G(z_type z){ return auzex(exp(z));}
  +
*/
  +
#include "ado.cin"
  +
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
  +
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
  +
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; FILE *o;o=fopen("traplot.eps","w"); ado(o,504,806);
  +
fprintf(o,"302 302 translate\n 100 100 scale\n");
  +
fprintf(o,"1 setlinejoin 2 setlinecap\n");
  +
for(n=-3;n<7;n++) {M(-3,n)L(2,n)}
  +
for(m=-3;m<3;m++) {M(m,-3)L(m,6)}
  +
M(0,M_E)L(1,M_E)
  +
M(0,M_E+1)L(1,M_E+1)
  +
fprintf(o,".004 W S\n");
  +
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(LambertW(x)));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".033 W 1 0 0 RGB S\n");
  +
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(x));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".04 W 1 .5 0 RGB S\n");
  +
// M(0,0) L(12.03,12.03) fprintf(o,".04 W 0 1 0 RGB S\n");
  +
DO(m,700){x=-3.02+.02*m; y=Re(tra(x)); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>10.03) break;} fprintf(o,".04 W 0 0 1 RGB S\n");
  +
DO(m,700){x=-3.02+.02*m; y=exp(x); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>10.03) break;} fprintf(o,".01 W 0 0 0 RGB S\n");
  +
  +
fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%'); fclose(o);
  +
system("epstopdf traplot.eps");
  +
system( "open traplot.pdf"); //for macintosh
  +
getchar(); system("killall Preview"); // For macintosh
  +
}
  +
</nowiki></nomathjax></poem>
  +
  +
==[[Latex]] generator of labelw==
  +
  +
<poem><nomathjax><nowiki>
  +
\documentclass[12pt]{article}
  +
\usepackage{geometry}
  +
\usepackage{graphicx}
  +
\usepackage{rotating}
  +
\paperwidth 506pt
  +
\paperheight 808pt
  +
\topmargin -105pt
  +
\oddsidemargin -73pt
  +
\textwidth 1100pt
  +
\textheight 1100pt
  +
\pagestyle {empty}
  +
\newcommand \sx {\scalebox}
  +
\newcommand \rot {\begin{rotate}}
  +
\newcommand \ero {\end{rotate}}
  +
\newcommand \ing {\includegraphics}
  +
\parindent 0pt
  +
\pagestyle{empty}
  +
\begin{document}
  +
\begin{picture}(604,804)
  +
%\put(10,10){\ing{PowPlo}}
  +
\put(0,0){\ing{traplot}}
  +
\put(280,784){\sx{3.4}{$y$}}
  +
\put(280,693){\sx{3.4}{$4$}}
  +
\put(224,666){\sx{3.4}{$1\!+\!\rm e$}}
  +
\put(280,593){\sx{3.4}{$3$}}
  +
\put(280,566){\sx{3.4}{$\rm e$}}
  +
\put(280,493){\sx{3.4}{$2$}}
  +
\put(280,393){\sx{3.4}{$1$}}
  +
\put(280,294){\sx{3.4}{$0$}}
  +
\put(252,191){\sx{3.4}{$-1$}}
  +
\put(252,091){\sx{3.4}{$-2$}}
  +
\put(070,272){\sx{3.4}{$-2$}}
  +
\put(170,272){\sx{3.4}{$-1$}}
  +
\put(294,272){\sx{3.4}{$0$}}
  +
\put(394,272){\sx{3.4}{$1$}}
  +
%\put(497,308){\sx{2.4}{$2$}}
  +
\put(482,274){\sx{3.4}{$x$}}
  +
  +
\put(24,342){\sx{3.4}{$y\!=\!\exp(x)$}}
  +
\put(56,42){\sx{3.4}{$y\!=\!\mathrm{tra}(x)$}}
  +
  +
\end{picture}
  +
\end{document}
  +
  +
</nowiki></nomathjax></poem>
  +
  +
[[Category:Book]]
  +
[[Category:BookPlot]]
  +
[[Category:C++]]
  +
[[Category:Elementary function]]
  +
[[Category:Explicit plot]]
  +
[[Category:Latex]]
  +
[[Category:Superfunction]]
  +
[[Category:Trapmann function]]

Latest revision as of 10:33, 20 July 2020

Explicit plot of the Trappmann function

$y=\mathrm{tra}(x)=\exp(x)\!+\!x$

For comparison, the exponent is shown,

$y=\exp(x)$

This function is interesting as a transfer function, because it has no fixed point. One of its superfunctions, namely, SuTra, is entire function with logarithmic asymptotic [1].

The image is used as Figure 20.1 in book Superfunction (In Russian, 2014; the English version is in preparation, 2015) [2].

References

  1. ↑ http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf D.Kouznetsov. Entire Function with Logarithmic Asymptotic. Applied Mathematical Sciences, Vol. 7, 2013, no. 131, 6527 - 6541
  2. ↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
    http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
    http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014

C++ generator of curves

Files ado.cin, should be loaded to the working directory in order to compile the code below


#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include<complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "Tania.cin" // need for LambertW
/*
#include "doya.cin" // need for LambertW
#include "LambertW.cin" // need for AuZex
#include "SuZex.cin"
#include "AuZex.cin"
*/
z_type tra(z_type z){ return exp(z)+z;}
/*
z_type F(z_type z){ return log(suzex(z));}
z_type G(z_type z){ return auzex(exp(z));}
*/
#include "ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; FILE *o;o=fopen("traplot.eps","w"); ado(o,504,806);
fprintf(o,"302 302 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
for(n=-3;n<7;n++) {M(-3,n)L(2,n)}
for(m=-3;m<3;m++) {M(m,-3)L(m,6)}
M(0,M_E)L(1,M_E)
M(0,M_E+1)L(1,M_E+1)
fprintf(o,".004 W S\n");
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(LambertW(x)));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".033 W 1 0 0 RGB S\n");
// DO(m,700){x=.01 +.02*m; y=Re(LambertW(x));if(m==0) M(x,y) else L(x,y) if(x>12.03||y>12.03) break;} fprintf(o,".04 W 1 .5 0 RGB S\n");
// M(0,0) L(12.03,12.03) fprintf(o,".04 W 0 1 0 RGB S\n");
DO(m,700){x=-3.02+.02*m; y=Re(tra(x)); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>10.03) break;} fprintf(o,".04 W 0 0 1 RGB S\n");
DO(m,700){x=-3.02+.02*m; y=exp(x); if(m==0) M(x,y) else L(x,y) if(x>3.03||y>10.03) break;} fprintf(o,".01 W 0 0 0 RGB S\n");

fprintf(o,"showpage\n"); fprintf(o,"%c%cTrailer\n",'%','%'); fclose(o);
      system("epstopdf traplot.eps");
      system( "open traplot.pdf"); //for macintosh
      getchar(); system("killall Preview"); // For macintosh
}

Latex generator of labelw


\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 506pt
\paperheight 808pt
\topmargin -105pt
\oddsidemargin -73pt
\textwidth 1100pt
\textheight 1100pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document}
\begin{picture}(604,804)
%\put(10,10){\ing{PowPlo}}
\put(0,0){\ing{traplot}}
\put(280,784){\sx{3.4}{$y$}}
\put(280,693){\sx{3.4}{$4$}}
\put(224,666){\sx{3.4}{$1\!+\!\rm e$}}
\put(280,593){\sx{3.4}{$3$}}
\put(280,566){\sx{3.4}{$\rm e$}}
\put(280,493){\sx{3.4}{$2$}}
\put(280,393){\sx{3.4}{$1$}}
\put(280,294){\sx{3.4}{$0$}}
\put(252,191){\sx{3.4}{$-1$}}
\put(252,091){\sx{3.4}{$-2$}}
\put(070,272){\sx{3.4}{$-2$}}
\put(170,272){\sx{3.4}{$-1$}}
\put(294,272){\sx{3.4}{$0$}}
\put(394,272){\sx{3.4}{$1$}}
%\put(497,308){\sx{2.4}{$2$}}
\put(482,274){\sx{3.4}{$x$}}

\put(24,342){\sx{3.4}{$y\!=\!\exp(x)$}}
\put(56,42){\sx{3.4}{$y\!=\!\mathrm{tra}(x)$}}

\end{picture}
\end{document}

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:14, 1 December 2018Thumbnail for version as of 06:14, 1 December 2018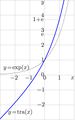1,050 × 1,677 (166 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:TraplotT.jpg&oldid=34821"