Difference between revisions of "File:ArcLambertWplot.png"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{oq|ArcLambertWplot.png|}} |
||
| − | #REDIRECT [[File:ZexPlot.png]] |
||
| + | |||
| + | [[Explicit plot]] of the [[LambertW function|ArcLambertW]] function, |
||
| + | |||
| + | \(\mathrm{ArcLambertW}(x)=x\cdot \exp(x) \) |
||
| + | |||
| + | The same [[ArcLambertW]] is denoted also with shorter symbol «[[zex]]». |
||
| + | |||
| + | This picture is used as Fig.11.1 in book |
||
| + | [[Superfunctions]] |
||
| + | <ref> |
||
| + | https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 |
||
| + | Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics Paperback – July 28, 2020 |
||
| + | English Edition by Dmitrii Kouznetsov (著) |
||
| + | Tools for evaluation of superfunctions, abelfunctions and non-integer iterates of holomorphic functions are collected. For a given transferfunction T, the superfunction is solution F of the transfer equation F(z+1)=T(F(z)) . The abelfunction is inverse of F. In particular, superfunctions of factorial, exp, sin are suggested. The Holomorphic extensions of the logistic sequence and those of the Ackermann functions are considered. Among ackermanns, the tetration (mainly to the base b>1) and natural pentation (to base b=e) are presented. The efficient algorithm for the evaluation of superfunctions and abelfunctions are described. The graphics and complex maps are plotted. The possible applications are discussed. Superfunctions significantly extend the set of functions, that can be used in scientific research and technical design. Generators of figures are loaded to http://mizugadro.mydns.jp/BOOK for the free downloading. With these generators, the Readers can reproduce (and modify) the figures from the Book. The Book is intended to be applied and popular. I try to avoid the complicated formulas, but some knowledge of the complex arithmetics and the Cauchy integral should help. |
||
| + | </ref><ref> |
||
| + | https://mizugadro.mydns.jp/BOOK/466.pdf |
||
| + | Dmitrii Kouznetsov. Superfunctions. LAP, 2020. |
||
| + | </ref>, Chapter 11, page 135. |
||
| + | |||
| + | ==Generators== |
||
| + | |||
| + | ===[[C++]] generator of the curve=== |
||
| + | |||
| + | // File [[ado.cin]] |
||
| + | <pre> |
||
| + | void ado(FILE *O, int X, int Y) |
||
| + | { fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%'); |
||
| + | fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y); |
||
| + | fprintf(O,"/M {moveto} bind def\n"); |
||
| + | fprintf(O,"/L {lineto} bind def\n"); |
||
| + | fprintf(O,"/S {stroke} bind def\n"); |
||
| + | fprintf(O,"/s {show newpath} bind def\n"); |
||
| + | fprintf(O,"/C {closepath} bind def\n"); |
||
| + | fprintf(O,"/F {fill} bind def\n"); |
||
| + | fprintf(O,"/o {.1 0 360 arc C S} bind def\n"); |
||
| + | fprintf(O,"/times-Roman findfont 20 scalefont setfont\n"); |
||
| + | fprintf(O,"/W {setlinewidth} bind def\n"); |
||
| + | fprintf(O,"/RGB {setrgbcolor} bind def\n");} |
||
| + | </pre> |
||
| + | //should be loaded (if not yet loaded) to the current directory in order to compile the code below: |
||
| + | <pre> |
||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include"ado.cin" |
||
| + | #define M(x,y) fprintf(o,"%5.3f %5.3f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%5.3f %5.3f L\n",0.+x,0.+y); |
||
| + | |||
| + | main(){ int j,k,m,n; DB x,y, a; |
||
| + | FILE *o;o=fopen("arclambertw.eps","w");ado(o,410,408); |
||
| + | fprintf(o,"304 104 translate\n 100 100 scale\n"); |
||
| + | for(m=-3;m<2;m++){ M(m,-1)L(m,3)} |
||
| + | for(n=-1;n<4;n++){ M(-3,n)L(1,n)} |
||
| + | fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | for(n=0;n<410;n+=2){x=-3.02+.01*n; y=x*exp(x); if(n==0)M(x,y) else L(x,y) } |
||
| + | fprintf(o,".03 W 0 .8 0 RGB S\n"); |
||
| + | M( 1, M_E) L(0, M_E) |
||
| + | M(-1,-1./M_E) L(0,-1./M_E) |
||
| + | fprintf(o,".005 W 0 0 0 RGB S\n"); |
||
| + | fprintf(o,"showpage\n%cTrailer",'%'); fclose(o); |
||
| + | system("epstopdf arclambertw.eps"); |
||
| + | system( "open arclambertw.pdf"); //these 2 commands may be specific for macintosh |
||
| + | getchar(); system("killall Preview");// if run at another operational sysetm, may need to modify |
||
| + | } |
||
| + | </pre> |
||
| + | |||
| + | ===[[Latex]] generator of the lables=== |
||
| + | <pre> |
||
| + | % Copyleft 2011 by Dmitrii Kouznetsov%<br> |
||
| + | \documentclass[12pt]{article} %<br> |
||
| + | \usepackage{geometry} %<br> |
||
| + | \usepackage{graphicx} %<br> |
||
| + | \usepackage{rotating} %<br> |
||
| + | \paperwidth 410pt %<br> |
||
| + | \paperheight 404pt %<br> |
||
| + | \topmargin -103pt %<br> |
||
| + | \oddsidemargin -94pt %<br> |
||
| + | \textwidth 1200pt %<br> |
||
| + | \textheight 600pt %<br> |
||
| + | \pagestyle {empty} %<br> |
||
| + | \newcommand \sx {\scalebox} %<br> |
||
| + | \newcommand \rot {\begin{rotate}} %<br> |
||
| + | \newcommand \ero {\end{rotate}} %<br> |
||
| + | \newcommand \ing {\includegraphics} %<br> |
||
| + | \begin{document} %<br> |
||
| + | { \begin{picture}(408,410) %<br> |
||
| + | \put(1,9){\ing{arclambertw}} %<br> |
||
| + | \put(288,398){\sx{2.9}{$y$}} %<br> |
||
| + | \put(309,378){\sx{3.1}{$\mathrm e$}} %<br> |
||
| + | \put(288,303){\sx{2.8}{$2$}} %<br> |
||
| + | \put(288,203){\sx{2.8}{$1$}} %<br> |
||
| + | \put(288,103){\sx{2.8}{$0$}} %<br> |
||
| + | \put(309,70){\sx{2.6}{$-\!1/\mathrm e$}} %<br> |
||
| + | \put( 86, 90){\sx{2.5}{$-\!2$}} %<br> |
||
| + | \put(186,90){\sx{2.5}{$-\!1$}} %<br> |
||
| + | % \put(300,-9){\sx{2.5}{$0$}} %<br> |
||
| + | \put(398,90){\sx{2.6}{$x$}} %<br> |
||
| + | \end{picture} %<br> |
||
| + | } %<br> |
||
| + | \end{document} |
||
| + | </pre> |
||
| + | ==References== |
||
| + | {{ref}} |
||
| + | |||
| + | https://mizugadro.mydns.jp/BOOK/466.pdf D.Kouznetov. Superfunctions. 2020. |
||
| + | |||
| + | 2020.07.28. |
||
| + | https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 |
||
| + | Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics Paperback – July 28, 2020 |
||
| + | English Edition by Dmitrii Kouznetsov (著) |
||
| + | |||
| + | {{fer}} |
||
| + | |||
| + | ==Keywords== |
||
| + | «[[]]», |
||
| + | «[[ArcLambertW]]», |
||
| + | «[[C++]]», |
||
| + | «[[Latex]]», |
||
| + | «[[Superfunctions]]», |
||
| + | «[[zex]]», |
||
| + | |||
| + | [[Category:Book]] |
||
| + | [[Category:BookPlot]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Elementary function]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:Explicit plots]] |
||
| + | [[Category:LambertW]] |
||
| + | [[Category:LambertW function]] |
||
| + | [[Category:Latex]] |
||
| + | [[Category:Inverse functions]] |
||
| + | [[Category:Special functions]] |
||
| + | [[Category:Zex]] |
||
Latest revision as of 17:02, 4 May 2025
Explicit plot of the ArcLambertW function,
\(\mathrm{ArcLambertW}(x)=x\cdot \exp(x) \)
The same ArcLambertW is denoted also with shorter symbol «zex».
This picture is used as Fig.11.1 in book Superfunctions [1][2], Chapter 11, page 135.
Generators
C++ generator of the curve
// File ado.cin
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//should be loaded (if not yet loaded) to the current directory in order to compile the code below:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include"ado.cin"
#define M(x,y) fprintf(o,"%5.3f %5.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%5.3f %5.3f L\n",0.+x,0.+y);
main(){ int j,k,m,n; DB x,y, a;
FILE *o;o=fopen("arclambertw.eps","w");ado(o,410,408);
fprintf(o,"304 104 translate\n 100 100 scale\n");
for(m=-3;m<2;m++){ M(m,-1)L(m,3)}
for(n=-1;n<4;n++){ M(-3,n)L(1,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");
for(n=0;n<410;n+=2){x=-3.02+.01*n; y=x*exp(x); if(n==0)M(x,y) else L(x,y) }
fprintf(o,".03 W 0 .8 0 RGB S\n");
M( 1, M_E) L(0, M_E)
M(-1,-1./M_E) L(0,-1./M_E)
fprintf(o,".005 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
system("epstopdf arclambertw.eps");
system( "open arclambertw.pdf"); //these 2 commands may be specific for macintosh
getchar(); system("killall Preview");// if run at another operational sysetm, may need to modify
}
Latex generator of the lables
% Copyleft 2011 by Dmitrii Kouznetsov%<br>
\documentclass[12pt]{article} %<br>
\usepackage{geometry} %<br>
\usepackage{graphicx} %<br>
\usepackage{rotating} %<br>
\paperwidth 410pt %<br>
\paperheight 404pt %<br>
\topmargin -103pt %<br>
\oddsidemargin -94pt %<br>
\textwidth 1200pt %<br>
\textheight 600pt %<br>
\pagestyle {empty} %<br>
\newcommand \sx {\scalebox} %<br>
\newcommand \rot {\begin{rotate}} %<br>
\newcommand \ero {\end{rotate}} %<br>
\newcommand \ing {\includegraphics} %<br>
\begin{document} %<br>
{ \begin{picture}(408,410) %<br>
\put(1,9){\ing{arclambertw}} %<br>
\put(288,398){\sx{2.9}{$y$}} %<br>
\put(309,378){\sx{3.1}{$\mathrm e$}} %<br>
\put(288,303){\sx{2.8}{$2$}} %<br>
\put(288,203){\sx{2.8}{$1$}} %<br>
\put(288,103){\sx{2.8}{$0$}} %<br>
\put(309,70){\sx{2.6}{$-\!1/\mathrm e$}} %<br>
\put( 86, 90){\sx{2.5}{$-\!2$}} %<br>
\put(186,90){\sx{2.5}{$-\!1$}} %<br>
% \put(300,-9){\sx{2.5}{$0$}} %<br>
\put(398,90){\sx{2.6}{$x$}} %<br>
\end{picture} %<br>
} %<br>
\end{document}
References
- ↑ https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics Paperback – July 28, 2020 English Edition by Dmitrii Kouznetsov (著) Tools for evaluation of superfunctions, abelfunctions and non-integer iterates of holomorphic functions are collected. For a given transferfunction T, the superfunction is solution F of the transfer equation F(z+1)=T(F(z)) . The abelfunction is inverse of F. In particular, superfunctions of factorial, exp, sin are suggested. The Holomorphic extensions of the logistic sequence and those of the Ackermann functions are considered. Among ackermanns, the tetration (mainly to the base b>1) and natural pentation (to base b=e) are presented. The efficient algorithm for the evaluation of superfunctions and abelfunctions are described. The graphics and complex maps are plotted. The possible applications are discussed. Superfunctions significantly extend the set of functions, that can be used in scientific research and technical design. Generators of figures are loaded to http://mizugadro.mydns.jp/BOOK for the free downloading. With these generators, the Readers can reproduce (and modify) the figures from the Book. The Book is intended to be applied and popular. I try to avoid the complicated formulas, but some knowledge of the complex arithmetics and the Cauchy integral should help.
- ↑ https://mizugadro.mydns.jp/BOOK/466.pdf Dmitrii Kouznetsov. Superfunctions. LAP, 2020.
https://mizugadro.mydns.jp/BOOK/466.pdf D.Kouznetov. Superfunctions. 2020.
2020.07.28. https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics Paperback – July 28, 2020 English Edition by Dmitrii Kouznetsov (著)
Keywords
«[[]]», «ArcLambertW», «C++», «Latex», «Superfunctions», «zex»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 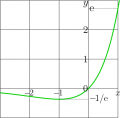 | 408 × 402 (10 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following file is a duplicate of this file (more details):
The following page uses this file: