Difference between revisions of "File:Z2itmapT.jpg"
| (One intermediate revision by one other user not shown) | |||
| Line 4: | Line 4: | ||
==[[C++]] generator of curves== |
==[[C++]] generator of curves== |
||
| − | // <poem><nomathjax><nowiki> |
+ | // <poem><nomathjax><nowiki>#include <math.h> |
| + | #include <stdio.h> |
||
| − | // C++ |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | //using namespace std; |
||
| + | #include<complex> |
||
| + | typedef std::complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "conto.cin" |
||
| + | |||
| + | DB c=2.; |
||
| + | // z_type F(z_type z) {return (c-1.)/(pow(2.,z)-c);} |
||
| + | z_type F(z_type z) {return pow(z,c);} |
||
| + | |||
| + | int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd; |
||
| + | int M=501,M1=M+1; |
||
| + | int N=501,N1=N+1; |
||
| + | DB X[M1],Y[N1]; DB *g, *f, *w; // w is working array. |
||
| + | g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB))); |
||
| + | f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB))); |
||
| + | w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB))); |
||
| + | char v[M1*N1]; // v is working array |
||
| + | FILE *o;o=fopen("z2itmap.eps","w"); ado(o,1002,1002); |
||
| + | fprintf(o,"501 501 translate\n 100 100 scale\n"); |
||
| + | fprintf(o,"1 setlinejoin 2 setlinecap\n"); |
||
| + | DO(m,M1) X[m]=-5+.02*(m-.5); |
||
| + | DO(n,N1) Y[n]=-5+.02*(n-.5); |
||
| + | //for(n=0;n<N1;n++) { Y[n]=1.09*sinh((3./200.)*(n-200)); printf("%3d %9.6f\n",n,Y[n]); } |
||
| + | for(m=-10;m<11;m++){M(m,-5) L(m,5) } |
||
| + | for(n=-10;n<11;n++){M( -5,n) L(5,n)} |
||
| + | fprintf(o,".006 W 0 0 0 RGB S\n"); |
||
| + | DO(m,M1)DO(n,N1){ g[m*N1+n]=999; |
||
| + | f[m*N1+n]=999;} |
||
| + | DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x); |
||
| + | DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019) |
||
| + | c=F(z); |
||
| + | // p=abs(c-z)/(abs(c)+abs(z)); p=-log(p)/log(10.); if(p>0 && p<17) g[m*N1+n]=p; |
||
| + | p=Re(c); q=Im(c); if(p>-99 && p<99 ){ g[m*N1+n]=p;f[m*N1+n]=q;} |
||
| + | }} |
||
| + | fprintf(o,"1 setlinejoin 1 setlinecap\n"); |
||
| + | p=1.2;q=.4; |
||
| + | |||
| + | for(m=-5;m<5;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".01 W 0 .6 0 RGB S\n"); |
||
| + | for(m=0;m<5;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".01 W .8 0 0 RGB S\n"); |
||
| + | for(m=0;m<5;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".01 W 0 0 .8 RGB S\n"); |
||
| + | for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n"); |
||
| + | for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n"); |
||
| + | conto(o,f,w,v,X,Y,M,N, (0. ),-2*p,2*p); fprintf(o,".02 W .5 0 .5 RGB S\n"); |
||
| + | for(m=-10;m<11;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n"); |
||
| + | // fprintf(o,"0 setlinejoin 0 setlinecap\n"); |
||
| + | // M(-10,0)L(0,0) fprintf(o,"1 1 1 RGB .02 W S\n"); |
||
| + | //#include "plofu.cin" |
||
| + | fprintf(o,"showpage\n"); |
||
| + | fprintf(o,"%c%cTrailer\n",'%','%'); |
||
| + | fclose(o); free(f); free(g); free(w); |
||
| + | system("epstopdf z2itmap.eps"); |
||
| + | system( "open z2itmap.pdf"); //for macintosh |
||
| + | getchar(); system("killall Preview"); // For macintosh |
||
| + | } |
||
// </nowiki></nomathjax></poem> |
// </nowiki></nomathjax></poem> |
||
| Line 64: | Line 124: | ||
\end{document} |
\end{document} |
||
%</nowiki></nomathjax></poem> |
%</nowiki></nomathjax></poem> |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
[[Category:Book]] |
[[Category:Book]] |
||
| + | [[Category:BookMap]] |
||
[[Category:Complex map]] |
[[Category:Complex map]] |
||
[[Category:Elementary function]] |
[[Category:Elementary function]] |
||
Latest revision as of 08:57, 1 December 2018
Complex map of function $T(z)=z^2$.
$\mu+\mathrm i \nu=T(x+\mathrm i y)$
C++ generator of curves
//
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include<complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
DB c=2.;
// z_type F(z_type z) {return (c-1.)/(pow(2.,z)-c);}
z_type F(z_type z) {return pow(z,c);}
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=501,M1=M+1;
int N=501,N1=N+1;
DB X[M1],Y[N1]; DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("z2itmap.eps","w"); ado(o,1002,1002);
fprintf(o,"501 501 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-5+.02*(m-.5);
DO(n,N1) Y[n]=-5+.02*(n-.5);
//for(n=0;n<N1;n++) { Y[n]=1.09*sinh((3./200.)*(n-200)); printf("%3d %9.6f\n",n,Y[n]); }
for(m=-10;m<11;m++){M(m,-5) L(m,5) }
for(n=-10;n<11;n++){M( -5,n) L(5,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999;
f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
c=F(z);
// p=abs(c-z)/(abs(c)+abs(z)); p=-log(p)/log(10.); if(p>0 && p<17) g[m*N1+n]=p;
p=Re(c); q=Im(c); if(p>-99 && p<99 ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=1.2;q=.4;
for(m=-5;m<5;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".01 W 0 .6 0 RGB S\n");
for(m=0;m<5;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".01 W .8 0 0 RGB S\n");
for(m=0;m<5;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".01 W 0 0 .8 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-2*p,2*p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-10;m<11;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
// fprintf(o,"0 setlinejoin 0 setlinecap\n");
// M(-10,0)L(0,0) fprintf(o,"1 1 1 RGB .02 W S\n");
//#include "plofu.cin"
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o); free(f); free(g); free(w);
system("epstopdf z2itmap.eps");
system( "open z2itmap.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
//
Latex generator of labels
%
\documentclass[12pt]{article}
\paperwidth 1044px
\paperheight 1036px
\textwidth 1204px
\textheight 1200px
\topmargin -86px
\oddsidemargin -72px
\usepackage{graphics}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \rmi {\mathrm{i}}
\parindent 0pt
\pagestyle{empty}
\begin{document}
\parindent 0pt
\sx{1}{\begin{picture}(1004,1004)
\put(40,20){\ing{z2itmap}}
\put(15,1008){\sx{3.3}{$y$}}
\put(15,910){\sx{3.3}{$4$}}
\put(15,810){\sx{3.3}{$3$}}
\put(15,710){\sx{3.3}{$2$}}
\put(15,610){\sx{3.3}{$1$}}
\put(15,510){\sx{3.3}{$0$}}
\put(-8,410){\sx{3.3}{$-1$}}
\put(-8,310){\sx{3.3}{$-2$}}
\put(-8,210){\sx{3.3}{$-3$}}
\put(-8,110){\sx{3.3}{$-4$}}
\put(-8,10){\sx{3.3}{$-5$}}
\put(8,-9){\sx{3.3}{$-5$}}
\put(108,-9){\sx{3.3}{$-4$}}
\put(208,-9){\sx{3.3}{$-3$}}
\put(308,-9){\sx{3.3}{$-2$}}
\put(408,-9){\sx{3.3}{$-1$}}
\put(534,-9){\sx{3.3}{$0$}}
\put(634,-9){\sx{3.3}{$1$}}
\put(734,-9){\sx{3.3}{$2$}}
\put(834,-9){\sx{3.3}{$3$}}
\put(934,-9){\sx{3.3}{$4$}}
\put(1026,-9){\sx{3.3}{$x$}}
\put(889,649){\sx{5}{\rot{-15}$\nu\!=\!10$\ero}}
\put(884,579){\sx{5}{\rot{-7}$\nu\!=\!5$\ero}}
\put(884,510){\sx{5}{$\nu\!=\!0$}}
\put(884,438){\sx{5}{\rot{6}$\nu\!=\!-5$\ero}}
\put(890,338){\sx{5}{\rot{-58}$\mu\!=\!10$\ero}}
\put(838,308){\sx{5}{\rot{-55}$\mu\!=\!5$\ero}}
\put(784,264){\sx{5}{\rot{-45}$\mu\!=\!0$\ero}}
\put(726,214){\sx{5}{\rot{-37}$\mu\!=\!-5$\ero}}
\put(706,154){\sx{5}{\rot{-33}$\mu\!=\!-10$\ero}}
\end{picture}}
\end{document}
%
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:39, 24 September 2013 | 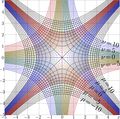 | 2,175 × 2,158 (1.74 MB) | T (talk | contribs) | Complex map of function $T(z)=z^2$. $\mu+\mathrm i \nu=T(x+\mathrm i y)$ ==C++ generator of curves== // <poem><nomathjax><nowiki> // C++ // </nowiki></nomathjax></poem> ==Latex generator of labels== % <poem><nomathjax><nowiki> % Latex %</now... |
You cannot overwrite this file.
File usage
The following page uses this file: