File:2015.01.03rudo.png
Original file (1,660 × 684 pixels, file size: 212 KB, MIME type: image/png)
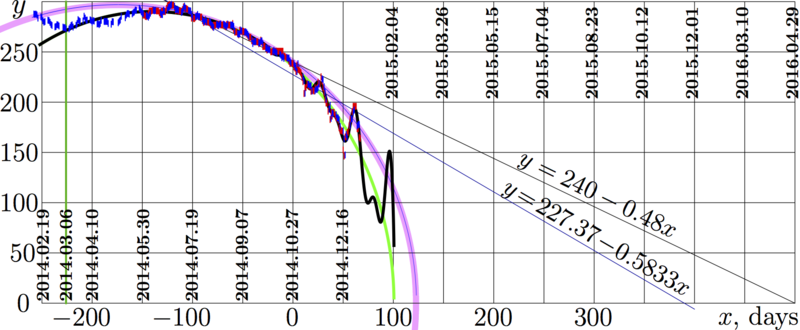
Value $y$ or 100 Russian roubles, measured in the USA cents, versus time $x$, measured in days since the beginning of the project, 2014.10.27.
Experimental data
The red sticks represent the experimental data by https://www.mataf.net/en/currency/converter-USD-RUB
The blue sticks represent the experimental data by www.cbr.ru/scripts/XML_dynamic.asp?date_req1=01/01/2014&date_req2=01/03/2015&VAL_NM_RQ=R01235
The mean square deviation between these two sets of data is about 3. This value is chosen as height of the sticks shown.
Linear approximations and pink arc
The upper linear approximation is from 2014.10.31, shown in also figure http://mizugadro.mydns.jp/t/index.php/File:Rusa2014.10.28t.jpg
The second linear fit $y=227.37−0.5833x$ made 2014.12.30 is shown also in figure http://mizugadro.mydns.jp/t/index.php/File:2014.12.31rudo.png
The pink arc follows the approximation $y=\sqrt{(123−x)(471+x)}$ , made 2014.10.29 and shown also in figure http://mizugadro.mydns.jp/t/index.php/File:RubleArc.png
Fitting of the experimental data
The green ellipse represents the approximation
$y=g(x)=1.20375 \sqrt{(100.639 - x)(381.547 + x)}$
The black oscillating curve shows the "advanced" fit
$y=h(x)=g(x)+ \exp(0.0319302 x) \Big( 1.88239\sin\big(0.348703(-93.3026 + x)\big) + 3.06092\sin\big(0.191964(-53.3159 + x)\big) \Big)$
Since 2014.03.06, the mean deviation of fit $h$ from the experimental data is smaller than 3, and the mean square deviation of fit $h$ from the experimental data is smaller than 4.
C++ generator of curves
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//#include"ado.cin"
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/O {5 0 360 arc C F} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//DB fit(DB x){ return 1.1882*sqrt((100.669 - x)*(389.828 + x));}
//DB fitos(DB x){ return fit(x) + 1.65997*exp(0.0477215*x)*sin(0.190509*(-53.7302 + x));} // 3.32858, 4.46385
//DB fit(DB x){ return 1.18052*sqrt((102.851 - x)*(388.552 + x));}
//DB fitos(DB x){ return fit(x) + 2.34457*exp(0.0379563*x)*sin(0.190307*(-54.7326 + x));} // 3.16919, 4.28327
//DB fit(DB x){ return 1.20375*sqrt((100.639 - x)*(381.547 + x));}
//DB fitos(DB x){ return fit(x) + exp(0.0319302*x)*
// (1.88239*sin(0.348703*(-93.3026 + x)) +
// 3.06092*sin(0.191964*(-53.3159 + x)) );} //, 2.87243, 3.92725}
DB fit(DB x){ return 1.19131*sqrt((102.09 - x)*(384.876 + x));}
DB fitos(DB x){ return fit(x) + exp(0.0390021*x)*
(1.05514*sin(0.407951*(-71.052 + x)) +
2.35622*sin(0.176673*(-55.1381+ x)));} // , 2.92204, 4.04111}
DB arc(DB x){return sqrt((123-x)*(471+x));}
DB lin0(DB x) {return 240.-.480*x;}
DB lin1(DB x) {return 227.37 - 0.583304*x;}
FILE *i,*o;
int main(){ int j,n,m,N,M; DB x,y,u,v,s,c;
o=fopen("15.eps","w"); ado(o,770,320);
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
#define O(x,y) fprintf(o,"%6.4f %6.4f O\n",0.+x,0.+y);
fprintf(o,"260 10 translate\n");
//fprintf(o,"460 10 translate\n");
for(n=0;n<301;n+=50) {M(-250,n)L(500,n)}
for(n=-250;n<501;n+=50) {M(n,0)L(n,300)}
fprintf(o,"0 0 0 RGB 2 setlinecap 1 setlinejoin .6 W S\n");
DO(n,8024){ x=-288+.1*n; y=arc(x); if(y>0) { if(n==0)M(x,y) else L(x,y)} else break;}
fprintf(o,"0 0 1 RGB .1 W S\n");
M(-150,lin0(-150)) L(500,lin0(500))
fprintf(o,"0 0 0 RGB .6 W S\n");
M(-150,lin1(-150)) L(400,lin1(400))
fprintf(o,"0 0 .6 RGB .6 W S\n");
//M(-235,0)L(-235,300) fprintf(o,"0 .7 0 RGB 2 W S\n");
//M(T[37],0)L(T[37],300) fprintf(o,"0 .7 0 RGB 2 W S\n");
M(-226,0)L(-226,300) fprintf(o,"0 .7 0 RGB 2 W S\n");
DO(n,4024){ x=-252+.1*n; y=fit(x); if(y>0) { if(n==0)M(x,y) else L(x,y)} else break;}
fprintf(o,"0 1 0 RGB 3 W S\n");
DO(n,4024){ x=-252+.1*n; y=fitos(x); if(y>0) { if(n==0)M(x,y) else L(x,y)} else break;}
fprintf(o,"0 0 0 RGB 3 W S\n");
DB X[1024],Y[1024];
DB T[1024],F[1024];
//i=fopen("ddat.txt","r");
fprintf(o,"1 0 0 RGB 1 setlinecap\n");
i=fopen("ddat.txt","r");
DO(n,1024){j=fscanf(i,"%d%lf",&m,&y); X[n]=x=m; Y[n]=y; if(j<2) break;
M(x,y-3) L(x,y+3);
}
fclose(i); N=n; printf("N=%3d\n",N);
fprintf(o,"1 W S\n");
fclose(i);
fprintf(o,"0 0 1 RGB 1 setlinecap\n");
i=fopen("datao.txt","r");
//i=fopen("ddat.txt","r");
DO(n,1024){j=fscanf(i,"%d%lf",&m,&y); T[n]=x=m; F[n]=y; if(j<2) break;
M(x,y-3)L(x,y+3);
//if(n==0)M(x,y) else L(x,y);
}
fclose(i); M=n; printf("M=%3d\n",M);
fprintf(o,"1 W S\n");
fclose(i);
s=c=0.;
DO(m,N){if (X[m] >= -236) break;}
int K=0;
for(n=m;n<N;n++){ x=X[n]; y=Y[n]; u=fitos(x); v=u-y; s+=fabs(v); c+=v*v; K++;}
s/=K; c/=K; c=sqrt(c);
printf("%8.4f %8.4f K=%3d\n",s,c, K);
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf 15.eps");
system( "open 15.pdf");
}
Latex generator of lalels
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\usepackage{color}
\definecolor{pink}{RGB}{255,160,255}
\paperwidth 800pt
\paperheight 330pt
\textwidth 800pt
\textheight 400pt
\topmargin -92pt
\oddsidemargin -68pt
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{document}
\begin{picture}(800,306)
%\put(-4,20){\sx{14.9}{\color{pink} \circle{50}}}
\put(96,20){\sx{14.9}{\color{pink} \circle{50}}}
%\put(296,20){\sx{14.9}{\color{pink} \circle{50}}}
%\put(10,10){\includegraphics{dollarplot}}
\put(10,10){\includegraphics{15}}
%\put(-10,0){\circle(200)}
%\put(0,-40){\sx{16}{\color{magenta} \circle{50}}}
%\put(-4,308){\sx{1.3}{Ruble}}
%\put(-4,296){\sx{1.3}{in cents}}
%\put(-4,282){\sx{1.3}{of USA}}
\put(-10,310){\sx{2.4}{$y$}}
\put(-22,262){\sx{2.2}{250}}
\put(-22,212){\sx{2.2}{200}}
\put(-22,162){\sx{2.2}{150}}
\put(-22,112){\sx{2.2}{100}}
\put(-12,62){\sx{2.2}{50}}
\put(-5,12){\sx{2.2}{0}}
\put( 30,-2){\sx{2.2}{$-200$}}
\put(130,-2){\sx{2.2}{$-100$}}
\put(264,-2){\sx{2.2}{$0$}}
\put(352,-2){\sx{2.2}{$100$}}
\put(452,-2){\sx{2.2}{$200$}}
\put(552,-2){\sx{2.2}{$300$}}
%\put(600,-2){\sx{2.5}{$400$}}
\put(696,-1){\sx{2.2}{$x$, days}}
\put(27, 22){\sx{1.5}{\rot{90}{\bf 2014.02.19}\ero}}%
%\put(40, 122){\sx{1.5}{\rot{90}{\bf 2014.03.06}\ero}}%
\put(50, 22){\sx{1.5}{\rot{90}{\bf 2014.03.06}\ero}}%
\put( 76, 22){\sx{1.5}{\rot{90}{\bf 2014.04.10}\ero}}%
\put(127, 22){\sx{1.5}{\rot{90}{\bf 2014.05.30}\ero}}%
\put(176, 22){\sx{1.5}{\rot{90}{\bf 2014.07.19}\ero}}%
\put(226,22){\sx{1.5}{\rot{90}{\bf 2014.09.07}\ero}}%
\put(276,22){\sx{1.5}{\rot{90}{\bf 2014.10.27}\ero}}%
\put(326,22){\sx{1.5}{\rot{90}{\bf 2014.12.16}\ero}}
\put(376,224){\sx{1.5}{\rot{90}{\bf 2015.02.04}\ero}}
\put(426,224){\sx{1.5}{\rot{90}{\bf 2015.03.26}\ero}}
\put(476,224){\sx{1.5}{\rot{90}{\bf 2015.05.15}\ero}}
\put(526,224){\sx{1.5}{\rot{90}{\bf 2015.07.04}\ero}}
\put(576,224){\sx{1.5}{\rot{90}{\bf 2015.08.23}\ero}}
\put(626,224){\sx{1.5}{\rot{90}{\bf 2015.10.12}\ero}}
\put(676,224){\sx{1.5}{\rot{90}{\bf 2015.12.01}\ero}}
\put(726,224){\sx{1.5}{\rot{90}{\bf 2016.03.10}\ero}}
\put(776,224){\sx{1.5}{\rot{90}{\bf 2016.04.29}\ero}}
\put(496,160){\sx{2.1}{\rot{-26} $y = 240 - 0.48 x$\ero}}
\put(480,132){\sx{2.1}{\rot{-30} $y\!=\!227.37\! -\! 0.5833x$\ero}}
\end{picture}
\end{document}
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:09, 1 December 2018 | 1,660 × 684 (212 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
There are no pages that use this file.