File:Vladi06.jpg

From TORI
Revision as of 08:56, 1 December 2018 by Maintenance script (talk | contribs)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to navigation Jump to search

Original file ‎(1,741 × 791 pixels, file size: 418 KB, MIME type: image/jpeg)

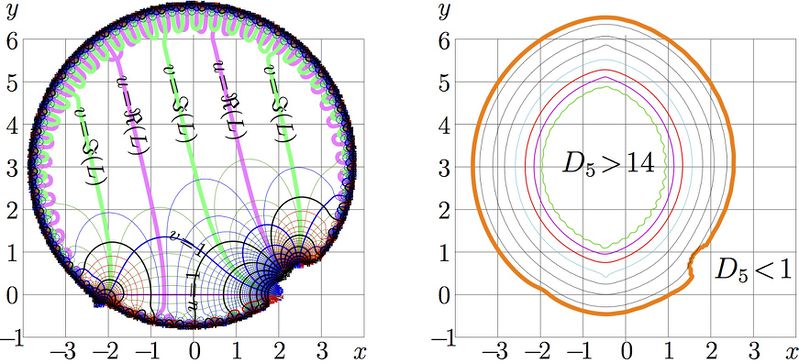
Complex map of the approximation "tai" of natural tetration, left, and the map of the corresponding agreement function $D$.

Left:

$u\!+\!\mathrm i v = \mathrm{tai}(x+\mathrm i y)$

Right:

$\displaystyle D_6=D_6(z)=-\lg\left( \frac

$ levels $D=1,2,4,6,8,10,12,14 ~ ~ $ are drawn. Level $D=1$ is drawn with thick line. Usage: this is figure 14.8 of the book Суперфункции (2014, In Russian) [1]
the English version is in preparation in 2015.
First time published in the Vladikavkaz Matehmatical Journal[2].

C++ generator of the first picture

fsexp.cin, ado.cin, conto.cin should be loaded in order to compile the code below


#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)

#include "fsexp.cin"
//#include "superex.cin"
//#include "superlo.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
z_type Zc=z_type(.31813150520476413,-1.3372357014306895);

  int M=201,M1=M+1;
  int N=201,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("figtai3.eps","w");ado(o,0,0,82,82);
FILE *o;o=fopen("vladi06a.eps","w");ado(o,82,82);
fprintf(o,"41 11 translate\n 10 10 scale\n");

DO(m,M1) X[m]=-4.+.04*(m-.5);
//DO(n,N1) Y[n]=-1.2 +.02*n*(1.+.000008*(n-8.)*(n-8));
DO(n,N1) Y[n]=-1. +.04*(n-.5);

//DB sy=6./sinh(.005*N);
//DO(n,N1) Y[n]=sy*sinh(.01*(n-N/2-.5+10));

for(m=-4;m<5;m++) { if(m==0){M(m,-1.1)L(m,6.1)}
                        else {M(m,-1)L(m,6)} }
for(n=-1;n<7;n++) {M( -4,n)L(4,n)} fprintf(o,".006 W 0 0 0 RGB S\n");

DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
                        f[m*N1+n]=9999; }
DO(m,M1){x=X[m]; printf("50 run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
                c=tai3(z);
                p=Re(c); q=Im(c);
                if(p>-9 && p<9) g[m*N1+n]=p;
                if(q>-9 && q<9) f[m*N1+n]=q;
        }}
p=1;q=.5;
conto(o,g,w,v,X,Y,M,N, ( Re(Zo) ),-q,q); fprintf(o,".1 W 1 .5 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( Im(Zo) ),-q,q); fprintf(o,".1 W .2 1 .5 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-Im(Zo) ),-q,q); fprintf(o,".1 W .5 1 .2 RGB S\n");

#include"plofu.cin"

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
        system("epstopdf vladi06a.eps");
        system( "open vladi06a.pdf");//for macintosh
// system( "xpdf fig06a.pdf");//for linux
//getchar(); system("killall Preview");//for macintosh
}

C++ generator of the second picture

fsexp.cin, ado.cin, conto.cin should be loaded in order to compile the code below


#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)

#include "fsexp.cin"
#include "conto.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//z_type Zo=z_type(.31813150520476413, 1.3372357014306895);
//z_type Zc=z_type(.31813150520476413,-1.3372357014306895);

  int M=200,M1=M+1;
  int N=201,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("figtai3L.eps","w");ado(o,0,0,82,82);
FILE *o;o=fopen("vladi06b.eps","w");ado(o,82,82);
fprintf(o,"41 11 translate\n 10 10 scale\n");

DO(m,M1) X[m]=-4.+.04*m;
DO(n,N1) Y[n]=-1.+.04*n;

//DB sy=6./sinh(.005*N);
//DO(n,N1) Y[n]=sy*sinh(.01*(n-N/2-.5+10));

for(m=-4;m<5;m++) { if(m==0){M(m,-1.1)L(m,6.1)}
                        else {M(m,-1)L(m,6)} }
for(n=-1;n<7;n++) {M( -4,n)L(4,n)} fprintf(o,".006 W 0 0 0 RGB S\n");

DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
                        f[m*N1+n]=9999; }
DO(m,M1){x=X[m]; printf("run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
        c=log(tai3(z+1.));
        d=tai3(z);
        p=abs(c-d);
        p=-log(p)/log(10.);
        if(p>-999 && p<999) g[m*N1+n]=p;
        }}
fprintf(o,"1 setlinecap 1 setlinejoin\n");

#include"plodi.cin"

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
        system("epstopdf vladi06b.eps");
        system( "open vladi06b.pdf"); //for macintosh
// system( "xpdf vladi06b.pdf"); //for linux
//getchar(); system("killall Preview");//for macintosh
}

Latex combiner


\documentclass[12pt]{article}
\usepackage{graphicx}
\usepackage{rotating}
\usepackage{geometry}
\paperwidth 418px
%\paperheight 134px
\paperheight 190px
\topmargin -108pt
\oddsidemargin -80pt
\pagestyle{empty}
\begin{document}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}

\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}

\newcommand \taiax {
\put(-3,77){\sx{.5}{$y$}}
\put(-3,69){\sx{.5}{$6$}}
\put(-3,59){\sx{.5}{$5$}}
\put(-3,49){\sx{.5}{$4$}}
\put(-3,39){\sx{.5}{$3$}}
\put(-3,29){\sx{.5}{$2$}}
\put(-3,19){\sx{.5}{$1$}}
\put(-3, 9){\sx{.5}{$0$}}
\put(-5,-1){\sx{.5}{$-\!1$}}
\put( 7 ,-4){\sx{.5}{$-\!3$}}
\put(17 ,-4){\sx{.5}{$-\!2$}}
\put(27 ,-4){\sx{.5}{$-\!1$}}
\put(40 , -4){\sx{.5}{$0$}}
\put(50 , -4){\sx{.5}{$1$}}
\put(60 , -4){\sx{.5}{$2$}}
\put(70 , -4){\sx{.5}{$3$}}
\put(78.8 , -4){\sx{.5}{$x$}}
}
\sx{2.23}{\begin{picture}(100,80)
%\put(0,0){\includegraphics{figtai3}}
\put(0,0){\includegraphics{vladi06a}}
\put(13,55){\sx{.44}{\rot{-77} $ v\!=\!\Im(L)$ \ero }}
\put(23,62.4){\sx{.44}{\rot{-77} $ u\!=\!\Re(L)$ \ero }}
\put(34,65){\sx{.44}{\rot{-76} $ v\!=\!\Im(L)$ \ero }}
\put(45.6,66){\sx{.44}{\rot{-76} $ u\!=\!\Re(L)$ \ero }}
\put(57.6,65){\sx{.44}{\rot{-77} $ v\!=\!\Im(L)$ \ero }}
%\put(33,5){\sx{.4}{\rot{67} $ v\!=\!\Im(L^*)$ \ero }}
\put(42,7){\sx{.4}{\rot{86} $ u\!=\!1$ \ero }}
\put(35,24.6){\sx{.4}{\rot{-31} $ v\!=\!1$ \ero }}
%\put(28,16){\sx{.4}{\rot{37} $ v\!=\!-1$ \ero }}
\taiax
\end{picture}}
\sx{2.23}{\begin{picture}(80,80)
%\put(0,0){\includegraphics{figtai3L}}
\put(0,0){\includegraphics{vladi06b}}
\taiax
\put(26,40){\sx{.58}{$D_{5}\!>\!14$}}
\put(62,15){\sx{.58}{$D_{5}\!<\!1$}}
\end{picture}}
\end{document}

References

  1. ↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
    http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
    http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014.
  2. ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. Figure 6.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:14, 1 December 2018Thumbnail for version as of 06:14, 1 December 20181,741 × 791 (418 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Vladi06.jpg&oldid=22218"